Regularization
[math] % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} % Machine Learning from Networked Data \newcommand{\nodesigvec}{\mathbf{u}} \newcommand{\edgesigvec}{\mathbf{f}} \newcommand{\edgesig}{f} \newcommand{\edgeweight}{A} \newcommand{\edgeweights}{\mA} \newcommand{\edgeidx}{e} \newcommand{\edgesigs}{\mathbb{R}^{\edges \times \featuredim}} \newcommand{\graph}{\mathcal{G}} \newcommand{\nodes}{\mathcal{V}} \newcommand{\degreemtx}{\mathbf{D}} \newcommand{\incidencemtx}{\mathbf{B}} \newcommand{\nodedegree}[1]{d^{(#1)}} \newcommand{\nodeidx}{i} \newcommand{\nrnodes}{n} \newcommand{\nodesigs}{\mathbb{R}^{\nodes \times \featuredim }} \newcommand{\naturalspace}{\mathcal{N}} \newcommand{\gindex}[1][i]{^{(#1)}} \newcommand{\gsignal}{\vw} \newcommand{\trueweights}{\overline{\vw}} \newcommand{\vt}{\mathbf{t}} \newcommand{\FIM}{\mathbf{F}} \newcommand{\FIMentry}{F} \newcommand{\edge}[2]{\{#1,#2\}} \newcommand{\directededge}[2]{\left(#1,#2\right)} [/math]
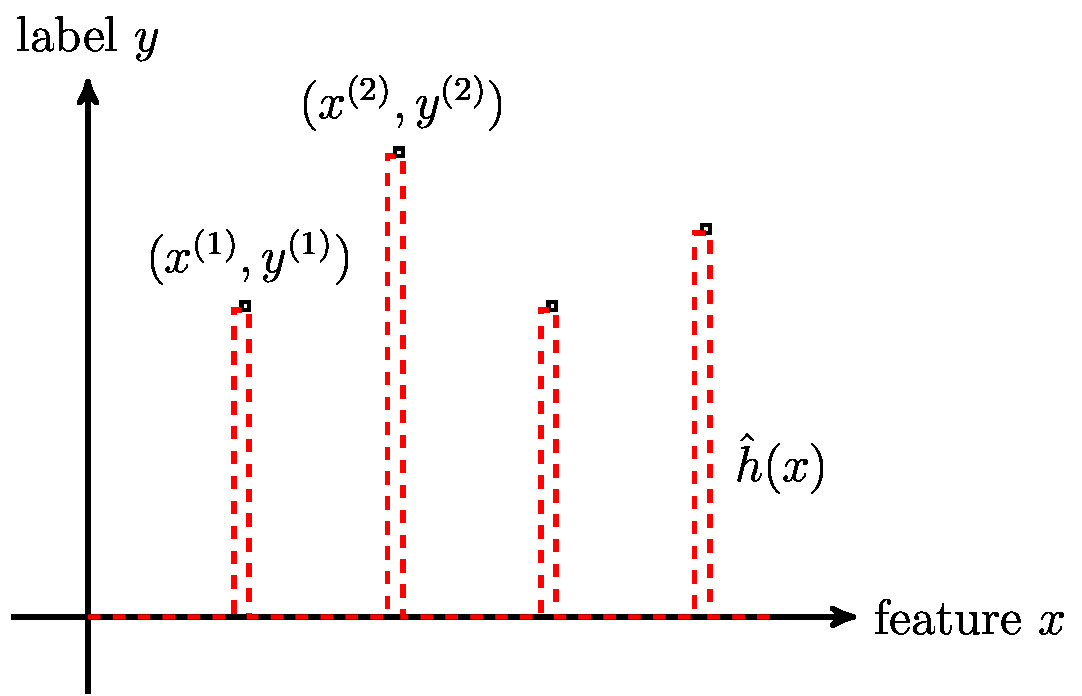
Many ML methods use the principle of empirical risk minimization (ERM) (see Chapter Empirical Risk Minimization ) to learn a hypothesis out of a hypothesis space by minimizing the average loss (training error) on a set of labeled data points (which constitute a training set). Using ERM as a guiding principle for ML methods makes sense only if the training error is a good indicator for its loss incurred outside the training set.
Figure fig_regular illustrates a typical scenario for a modern ML method which uses a large hypothesis space. This large hypothesis space includes highly non-linear maps which can perfectly resemble any dataset of modest size. However, there might be non-linear maps for which a small training error does not guarantee accurate predictions for the labels of data points outside the training set.
Chapter Model Validation and Selection discussed validation techniques to verify if a hypothesis with small training error will predict also well the labels of data points outside the training set. These validation techniques, including Algorithm alg:validated_ERM and Algorithm alg:kfoldCV_ERM, probe the hypothesis [math]\hat{h} \in \hypospace[/math] delivered by ERM on a validation set. The validation set consists of data points which have not been used in the training set of ERM . The validation error, which is the average loss of the hypothesis on the data points in the validation set, serves as an estimate for the average error or risk of the hypothesis [math]\hat{h}[/math].
This chapter discusses regularization as an alternative to validation techniques. In contrast to validation, regularization techniques do not require having a separate validation set which is not used for the ERM . This makes regularization attractive for applications where obtaining a separate validation set is difficult or costly (where labelled data is scarce).
Instead of probing a hypothesis [math]\hat{h}[/math] on a validation set, regularization techniques estimate (or approximate) the loss increase when applying [math]\hat{h}[/math] to data points outside the training set. The loss increase is estimated by adding a regularization term to the training error in ERM .
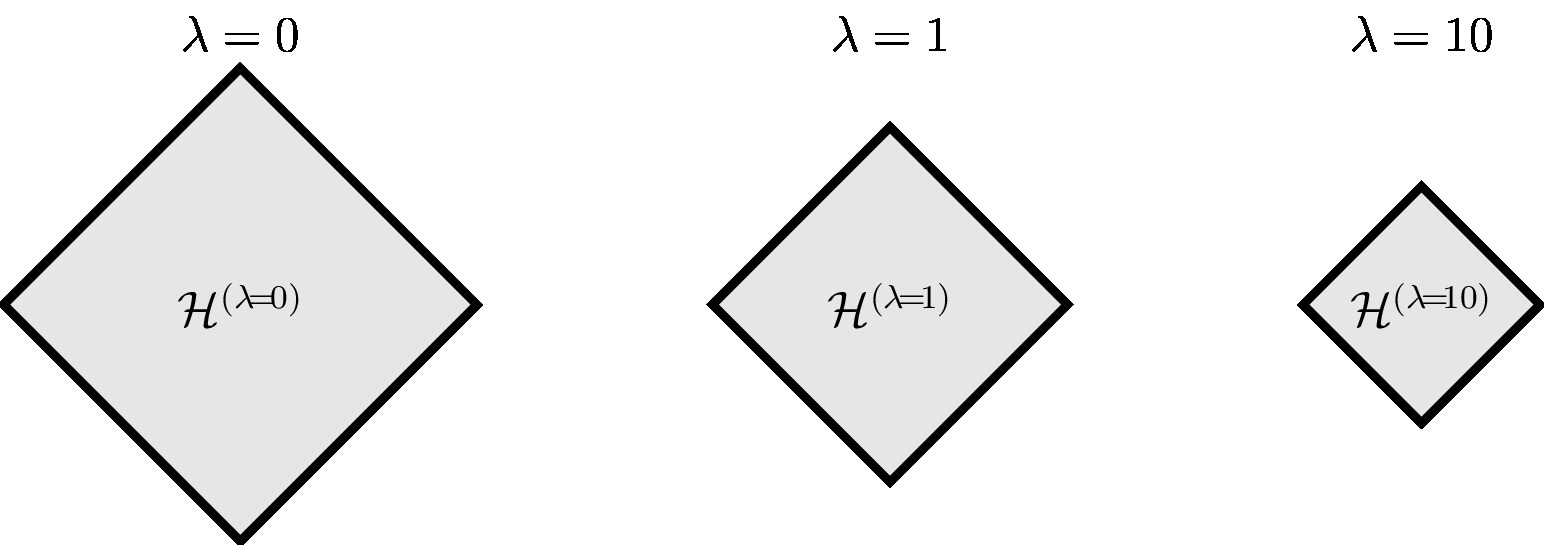
Section Structural Risk Minimization discusses the resulting regularized ERM, which we will refer to as structural risk minimization (SRM). It turns out that the SRM is equivalent to ERM using a smaller (pruned) hypothesis space. The amount of pruning depends on the weight of the regularization term relative to the training error. For an increasing weight of the regularization term, we obtain a stronger pruning resulting in a smaller effective hypothesis space.
Section Robustness constructs regularization terms by requiring the resulting ML method to be robust against (small) random perturbations of the data points in a training set. Here, we replace each data point of a training set by the realization of a random variable (RV) that fluctuates around this data point. This construction allows to interpret regularization as a (implicit) form of data augmentation.
Section Data Augmentation discusses data augmentation methods as a simulation-based implementation of regularization. Data augmentation adds a certain number of perturbed copies to each data point in the training set. One way to construct perturbed copies of a data point is to add the realization of a RV to its features.
Section Statistical and Computational Aspects of Regularization analyzes the effect of regularization for linear regression using a simple probabilistic model for data points. This analysis parallels our previous study of the validation error of linear regression in Section A Probabilistic Analysis of Generalization . Similar to Section A Probabilistic Analysis of Generalization , we reveal a trade-off between the bias and variance of the hypothesis learnt by regularized linear regression. This trade- off was traced out by a discrete model parameter (the effective dimension) in Section A Probabilistic Analysis of Generalization . In contrast, regularization offers a continuous trade-off between bias and variance via a continuous regularization parameter.
Semi-supervised learning (SSL) uses (large amounts of) unlabeled data points to support the learning of a hypothesis from (a small number of) labeled data points [1]. Section Semi-Supervised Learning discusses semi-supervised learning (SSL) methods that use the statistical properties of unlabeled data points to construct useful regularization terms. These regularization terms are then used in SRM with a (typically small) set of labeled data points.
Multitask learning exploits similarities between different but related learning tasks [2]. We can formally define a learning task by a particular choice for the loss function (see Section The Loss ) . The primary role of a loss function is to score the quality of a hypothesis map. However, the loss function also encapsulates the choice for the label of a data point. For learning tasks defined for a single underlying data generation process it is reasonable to assume that the same subset of features is relevant for those learning tasks. One example for a ML application involving several related learning tasks is multi-label classification (see Section Labels ). Indeed, each individual label of a data point represents an separate learning task. Section Multitask Learning shows how multitask learning can be implemented using regularization methods. The loss incurred in different learning tasks serves mutual regularization terms in a joint SRM for all learning tasks.
Section Transfer Learning shows how regularization can be used for transfer learning. Like multitask learning also transfer learning exploits relations between different learning tasks. In contrast to multitask learning, which jointly solves the individual learning tasks, transfer learning solves the learning tasks sequentially. The most basic form of transfer learning is to fine tune a pre-trained model. A pre-trained model can be obtained via ERM in a (“source”) learning task for which we have a large amount of labeled training data. The fine-tuning is then obtained via ERM in the (“target”) learning task of interest for which we might have only a small amount of labeled training data.
Structural Risk Minimization
Section The Model defined the effective dimension [math]\effdim{\hypospace}[/math] of a hypothesis space [math]\hypospace[/math] as the maximum number of data points that can be perfectly fit by some hypothesis [math]h \in \hypospace[/math]. As soon as the effective dimension of the hypothesis space in equ_def_ERM_funs exceeds the number [math]\samplesize[/math] of training data points, we can find a hypothesis that perfectly fits the training data. However, a hypothesis that perfectly fits the training data might deliver poor predictions for data points outside the training set (see Figure fig_regular).
Modern ML methods typically use a hypothesis space with large effective dimension [3][4]. Two well-known examples for such methods is linear regression (see Section Linear Regression ) using a large number of features and deep learning with artificial neural network (ANN)s using a large number (billions) of artificial neurons (see Section Deep Learning ). The effective dimension of these methods can be easily on the order of billions ([math]10^{9}[/math]) if not larger [5]. To avoid overfitting during the naive use of ERM we would require a training set containing at least as many data points as the effective dimension of the hypothesis space. However, in practice we often do not have access to a training set consisting of billions of labeled data points. The challenge is typically in the labelling process which often requires human labour.
It seems natural to combat overfitting of a ML method by pruning its hypothesis space [math]\hypospace[/math]. We prune [math]\hypospace[/math] by removing some of the hypothesis in [math]\hypospace[/math] to obtain the smaller hypothesis space [math]\hypospace' \subset \hypospace[/math]. We then replace ERM with the restricted (or pruned) ERM
The effective dimension of the pruned hypothesis space [math]\hypospace'[/math] is typically much smaller than the effective dimension of the original (large) hypothesis space [math]\hypospace[/math], [math]\effdim{\hypospace'} \ll \effdim{\hypospace}[/math].
For a given size [math]\samplesize[/math] of the training set, the risk of overfitting in \eqref{equ_ERM_fun_pruned} is
much smaller than the risk of overfitting in equ_def_ERM_funs .
Let us illustrate the idea of pruning for linear regression using the hypothesis space constituted by linear maps [math]h(\featurevec) = \weights^{T} \featurevec[/math]. The effective dimension of equ_lin_hypospace is equal to the number of features, [math]\effdim{\hypospace} = \featuredim[/math]. The hypothesis space [math]\hypospace[/math] might be too large if we use a large number [math]\featurelen[/math] of features, leading to overfitting. We prune equ_lin_hypospace by retaining only linear hypotheses [math]h(\featurevec) = \big(\weights'\big)^T \featurevec[/math] with parameter vectors [math]\weights'[/math] satisfying [math]\weight'_{3} = \weights_{4}'= \ldots = \weights_{\featurelen}'=0[/math]. Thus, the hypothesis space [math]\hypospace'[/math] is constituted by all linear maps that only depend on the first two features [math]\feature_{1},\feature_{2}[/math] of a data point. The effective dimension of [math]\hypospace'[/math] is dimension is [math]\effdim{\hypospace'}=2[/math] instead of [math]\effdim{\hypospace}=\featurelen[/math].
Pruning the hypothesis space is a special case of a more general strategy which we refer to as SRM [6]. The idea behind SRM is to modify the training error in ERM to favour hypotheses which are more smooth or regular in a specific sense. By enforcing a smooth hypothesis, a ML methods becomes less sensitive, or more robust, to small perturbations of data points in the training set. Section Robustness discusses the intimate relation between the robustness (against perturbations of the data points in the training set) of a ML method and its ability to generalize to data points outside the training set.
We measure the smoothness of a hypothesis using a regularizer [math]\regularizer(h) \in \mathbb{R}_{+}[/math]. Roughly speaking, the value [math]\regularizer(h)[/math] measures the irregularity or variation of a predictor map [math]h[/math]. The (design) choice for the regularizer depends on the precise definition of what is meant by regularity or variation of a hypothesis. Section Data Augmentation discusses how a particular choice for the regularizer [math]\regularizer(h)[/math] arises naturally from a probabilistic model for data points.
We obtain SRM by adding the scaled regularizer [math]\regparam \regularizer(h)[/math] to the ERM ,
We can interpret the penalty term [math]\regparam \regularizer(h)[/math] in \eqref{equ_ERM_fun_regularized} as an estimate (or approximation) for the increase, relative to the training error on [math]\dataset[/math], of the average loss of a hypothesis [math]\hat{h}[/math] when it is applied to data points outside [math]\dataset[/math]. Another interpretation of the term [math]\regparam \regularizer(h)[/math] will be discussed in Section Data Augmentation .
The regularization parameter [math]\regparam[/math] allows us to trade between a
small training error [math]\emperror(h^{(\vw)}|\dataset)[/math] and small regularization term [math]\regularizer(h)[/math], which
enforces smoothness or regularity of [math]h[/math]. If we choose a large value for [math]\regparam[/math], irregular or hypotheses [math]h[/math],
with large [math]\regularizer(h)[/math], are heavily “punished” in \eqref{equ_ERM_fun_regularized}. Thus,
increasing the value of [math]\regparam[/math] results in the solution (minimizer) of \eqref{equ_ERM_fun_regularized} having
smaller [math]\regularizer(h)[/math]. On the other hand, choosing a small value for [math]\regparam[/math] in \eqref{equ_ERM_fun_regularized} puts more
emphasis on obtaining a hypothesis [math]h[/math] incurring a small training error.
For the extreme case [math]\regparam =0[/math], the SRM \eqref{equ_ERM_fun_regularized} reduces to ERM.
The pruning approach \eqref{equ_ERM_fun_pruned} is intimately related to the SRM \eqref{equ_ERM_fun_regularized}. They are, in a certain sense, dual to each other. First, note that \eqref{equ_ERM_fun_regularized} reduces to the pruning approach \eqref{equ_ERM_fun_pruned} when using the regularizer [math]\regularizer(h) = 0[/math] for all [math]h \in \hypospace'[/math] , and [math]\regularizer(h) = \infty[/math] otherwise, in \eqref{equ_ERM_fun_regularized}. In the other direction, for many important choices for the regularizer [math]\regularizer(h)[/math], there is a restriction [math]\hypospace^{(\regparam)} \subset \hypospace[/math] such that the solutions of \eqref{equ_ERM_fun_pruned} and \eqref{equ_ERM_fun_regularized} coincide (see Figure fig_soft_pruning_regularization). The relation between the optimization problems \eqref{equ_ERM_fun_pruned} and \eqref{equ_ERM_fun_regularized} can be made precise using the theory of convex duality (see [7](Ch. 5) and [8]).
For a hypothesis space [math]\hypospace[/math] whose elements [math]h \in \hypospace[/math] are parametrized by
a parameter vector [math]\weights \in \mathbb{R}^{\featuredim}[/math], we can rewrite SRM \eqref{equ_ERM_fun_regularized} as
For the particular choice of squared squared error loss, linear hypothesis spaceand regularizer [math]\regularizer(\weights)=\| \weights \|_{2}^{2}[/math], SRM \eqref{equ_rerm_weight} specializes to
The special case \eqref{equ_rerm_ridge_regression} of SRM \eqref{equ_rerm_weight} is known
as ridge regression [9]. Ridge regression \eqref{equ_rerm_ridge_regression} is equivalent to (see [8](Ch. 5))
with the restricted hypothesis space
For any given value [math]\regparam[/math] of the regularization parameter in \eqref{equ_rerm_ridge_regression}, there is a number [math]C(\regparam)[/math] such that solutions of \eqref{equ_rerm_ridge_regression} coincide with the solutions of \eqref{equ_restr_ERM}. Thus, ridge regression \eqref{equ_rerm_ridge_regression} is equivalent to linear regression with a pruned version [math]\hypospace^{(\regparam)}[/math] of the linear hypothesis space. The size of the pruned hypothesis space [math]\hypospace^{(\regparam)}[/math] \eqref{equ_hyposapce_lambda} varies continuously with [math]\regparam[/math].
Another popular special case of ERM \eqref{equ_rerm_weight} is obtained for the regularizer [math]\regularizer(\weights)=\| \weights \|_{1}[/math]
and known as the Lasso [10]
Ridge regression \eqref{equ_rerm_ridge_regression} and the Lasso \eqref{equ_rerm_Lasso} have fundamentally different computational and statistical properties. Ridge regression \eqref{equ_rerm_ridge_regression} uses a smooth and convex objective function that can be minimized using efficient gradient descent (GD) methods. The objective function of Lasso \eqref{equ_rerm_Lasso} is also convex but non-smooth and therefore requires more advanced optimization methods. The increased computational complexity of Lasso \eqref{equ_rerm_Lasso} comes at the benefit of typically delivering a hypothesis with a smaller expected loss than those obtained from ridge regression [4][10].
Robustness
Section Structural Risk Minimization motivates regularization as a soft variant of model selection. Indeed, the regularization term in SRM \eqref{equ_ERM_fun_regularized} is equivalent to ERM \eqref{equ_ERM_fun_pruned} using a pruned (reducing) hypothesis space. We now discuss an alternative view on regularization as a means to make ML methods robust.
The ML methods discussed in Chapter Empirical Risk Minimization rest on the idealizing assumption that we have access to the true label values and feature values of labeled data points (that form a training set). These methods learn a hypothesis [math]h \in \hypospace[/math] with minimum average loss (training error) incurred for data points in the training set. In practice, the acquisition of label and feature values might be prone to errors. These errors might stem from the measurement device itself (hardware failures or thermal noise in electronic devices) or might be due to human mistakes such as labelling errors.
Let us assume for the sake of exposition that the label values [math]\truelabel^{(\sampleidx)}[/math] in the training set are accurate but that the features [math]\featurevec^{(\sampleidx)}[/math] are a perturbed version of the true features of the [math]\sampleidx[/math]th data point. Thus, instead of having observed the data point [math]\big( \featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)} \big)[/math] we could have equally well observed the data point [math]\big( \featurevec^{(\sampleidx)}+\bm{\varepsilon}, \truelabel^{(\sampleidx)} \big)[/math] in the training set. Here, we have modelled the perturbations in the features using a RV [math]\bm{\varepsilon}[/math]. The probability distribution of the perturbation [math]\bm{\varepsilon}[/math] is a design parameter that controls robustness properties of the overall ML method. We will study a particular choice for this distribution in Section Data Augmentation .
A robust ML method should learn a hypothesis that incurs a small loss not only for a specific data point [math]\big( \featurevec^{(\sampleidx)}, y^{(\sampleidx)} \big)[/math] but also for perturbed data points [math]\big( \featurevec^{(\sampleidx)}+\bm{\varepsilon}, y^{(\sampleidx)} \big)[/math]. Therefore, it seems natural to replace the loss [math]\loss{\big( \featurevec^{(\sampleidx)}, y^{(\sampleidx)} \big)}{h}[/math], incurred on the [math]\sampleidx[/math]th data point in the training set, with the expectation
The expectation \eqref{equ_def_expe_perturb_robust} is computed using the probability distribution of the perturbation [math]\bm{\varepsilon}[/math]. We will show in Section Data Augmentation that minimizing the average of the expectation \eqref{equ_def_expe_perturb_robust}, for [math]\sampleidx=1,\ldots,\samplesize[/math], is equivalent to the SRM \eqref{equ_ERM_fun_regularized}.
Using the expected loss \eqref{equ_def_expe_perturb_robust} is not the only possible approach to make a ML method robust. Another approach to make a ML method robust is known as bootstrap aggreation (bagging). The idea of bagging is to use the bootstrap method (see Section The Bootstrap and [9](Ch. 8)) to construct a finite number of perturbed copies [math]\dataset^{(1)},\ldots,\dataset^{(\augparam)}[/math] of the original training set [math]\dataset[/math].
We then learn (e.g, using ERM) a separate hypothesis [math]h^{(\augidx)}[/math] for each perturbed copy [math]\dataset^{(\augidx)}[/math], [math]\augidx = 1,\ldots, \augparam[/math]. This results in a whole ensemble of different hypotheses [math]h^{(\augidx)}[/math] which might even belong to different hypothesis spaces. For example, one the hypothesis [math]h^{(1)}[/math] could be a linear map (see Section Linear Regression ) and the hypothesis [math]h^{(2)}[/math] could be obtained from an ANN (see Section Deep Learning ).
The final hypothesis delivered by bagging is obtained by combining or aggregating (e.g., using the average) the predictions [math]h^{(\augidx)}\big(\featurevec\big)[/math] delivered by each hypothesis [math]h^{(\augidx)}[/math], for [math]\augidx=1,\ldots,\augparam[/math] in the ensemble. The ML method referred to as random forest uses bagging to learn an ensemble of decision trees (see Chapter Decision Trees ). The individual predictions obtained from the different decision trees forming a random forest are then combined (e.g., using an average for numeric labels or a majority vote for finite-valued labels), to obtain a final prediction [9].
Data Augmentation
ML methods using ERM are prone to overfitting as soon as the effective dimension of the hypothesis space [math]\hypospace[/math] exceeds the number [math]\samplesize[/math] of data points in the training set. Section Model Selection and Section Structural Risk Minimization approached this by modifying either the model or the loss function by adding a regularization term. Both approaches prune the hypothesis space [math]\hypospace[/math] underlying a ML method to reduce the effective dimension [math]\effdim{\hypospace}[/math]. Model selection does this reduction in a discrete fashion while regularization implements a soft “shrinking” of the hypothesis space.
Instead of trying to reduce the effective dimension we could also try to increase the number [math]\samplesize[/math] of data points in the training set used for ERM .
We now discuss how to synthetically generate new labeled data points by exploiting statistical symmetries of data.
The data arising in many ML applications exhibit intrinsic symmetries and invariances at least in some approximation. The rotated image of a cat still shows a cat. The temperature measurement taken at a given location will be similar to another measurement taken [math]10[/math] milliseconds later. Data augmentation exploits such symmetries and invariances to augment the raw data with additional synthetic data.
Let us illustrate data augmentation using an application that involves data points characterized by features [math]\featurevec \in \mathbb{R}^{\featuredim}[/math] and number labels [math]y \in \mathbb{R}[/math]. We assume that the data generating process is such that data points with close feature values have the same label. Equivalently, this assumption is requiring the resulting ML method to be robust against small perturbations of the feature values (see Section Robustness ). This suggests to augment a data point [math]\big(\featurevec,\truelabel\big)[/math] by several synthetic data points
with [math]{\bm \varepsilon}^{(1)},\ldots,{\bm \varepsilon}^{(\augparam)}[/math] being realizations of independent and identically distributed (iid) random vectors with the same probability distribution [math]p({\bm \varepsilon})[/math].
Given a (raw) dataset [math]\dataset = \big\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots, \big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big) \} [/math] we denote the associated augmented dataset by
The size of the augmented dataset [math]\dataset'[/math] is [math] \samplesize' = \augparam \times \samplesize[/math]. For a sufficiently large augmentation parameter [math]\augparam[/math], the augmented sample size [math]\samplesize'[/math] is larger than the effective dimension [math]\featurelen[/math] of the hypothesis space [math]\hypospace[/math]. We then learn a hypothesis via ERM on the augmented dataset,
We can interpret data-augmented ERM \eqref{equ_def_ERM_funs_aug} as a data-driven form of regularization (see Section Structural Risk Minimization ). The regularization is implemented by replacing, for each data point [math]\big(\featurevec^{(\sampleidx)},y^{(\sampleidx)}\big) \in \dataset[/math], the loss [math]\loss{(\featurevec^{(\sampleidx)},y^{(\sampleidx)})}{h}[/math] with the average loss [math](1/\augparam)\sum_{\augidx=1}^{\augparam} \loss{(\featurevec^{(\sampleidx)}+{\bm \varepsilon}^{(b)},y^{(\sampleidx)})}{h}[/math] over the augmented data points that accompany [math]\big(\featurevec^{(\sampleidx)},y^{(\sampleidx)}\big) \in \dataset[/math].
Note that in order to implement \eqref{equ_def_ERM_funs_aug} we need to first generate [math]\augparam[/math] realizations [math]{\bm \varepsilon}^{(b)} \in \mathbb{R}^{\featurelen}[/math] of iid random vectors with common probability distribution [math]p({\bm \varepsilon})[/math]. This might be computationally costly for a large [math]\augparam, \featurelen[/math]. However, when using a large augmentation parameter [math]\augparam[/math], we might use the approximation
This approximation is made precise by a key result of probability theory, known as the law of large numbers. We obtain an instance of ERM by inserting \eqref{equ_approx_augm_loss_expect} into \eqref{equ_def_ERM_funs_aug},
The usefulness of \eqref{equ_def_ERM_funs_aug_approx} as an approximation to the augmented
ERM \eqref{equ_def_ERM_funs_aug} depends on the difficulty of computing the expectation [math]\expect\big\{ \loss{(\featurevec^{(\sampleidx)}+{\bm \varepsilon},\truelabel^{(\sampleidx)})}{h} \big\}[/math]. The complexity of computing this expectation depends
on the choice of loss function and the choice for the probability distribution [math]p({\bm \varepsilon})[/math].
Let us study \eqref{equ_def_ERM_funs_aug_approx} for the special case linear regression with squared error loss and linear hypothesis space,
We use perturbations [math]{\bm \varepsilon}[/math] drawn a multivariate normal distribution with zero mean and covariance matrix [math]\sigma^{2} \mathbf{I}[/math],
We develop \eqref{equ_def_ERM_funs_aug_approx_linreg} further by using
The identity \eqref{equ_uncorr_augmentation_implicit} uses that the data points [math]\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)[/math] are fixed and known (deterministic) while [math]{\bm \varepsilon}[/math] is a zero-mean random vector. Combining \eqref{equ_uncorr_augmentation_implicit} with \eqref{equ_def_ERM_funs_aug_approx_linreg},
where the last step used [math]\expect \big\{ \sqeuclnorm { {\bm \varepsilon} } \big\} \stackrel{\eqref{equ_augm_mvn_standard}}{=} \featurelen \sigma^{2}[/math]. Inserting \eqref{equ_implicit_aug_regu_11} into \eqref{equ_def_ERM_funs_aug_approx_linreg},
We have obtained \eqref{equ_def_ERM_funs_aug_approx_ridge} as an approximation of the augmented ERM \eqref{equ_def_ERM_funs_aug} for the special case of squared error loss and the linear hypothesis space. This approximation uses the law of large numbers \eqref{equ_approx_augm_loss_expect} and becomes more accurate for increasing augmentation parameter [math]\augparam[/math].
Note that \eqref{equ_def_ERM_funs_aug_approx_ridge} is nothing but ridge regression \eqref{equ_rerm_ridge_regression} using the regularization parameter [math]\regparam =\featurelen \sigma^{2}[/math]. Thus, we can interpret ridge regression as implicit data augmentation \eqref{equ_def_augmented_dataset} by applying random perturbations \eqref{equ_def_copies_aug} to the feature vectors in the original training set [math]\dataset[/math].
The regularizer [math]\regularizer(\weights) = \sqeuclnorm{ \weights }[/math] in \eqref{equ_def_ERM_funs_aug_approx_ridge} arose naturally from the specific choice for the probability distribution \eqref{equ_augm_mvn_standard} of the random perturbation [math]{\bm \varepsilon}^{(\sampleidx)}[/math] in \eqref{equ_def_copies_aug} and using the squared error loss. Other choices for this probability distribution or the loss function result in different regularizers.
Augmenting data points with random perturbations distributed according \eqref{equ_augm_mvn_standard} treat the features of a data point independently. For application domains that generate data points with highly correlated features it might be useful to augment data points using random perturbations [math]{\bm \varepsilon}[/math] (see \eqref{equ_def_copies_aug}) distributed as
The covariance matrix [math]\mC[/math] of the perturbation [math]{\bm \varepsilon}[/math] can be chosen using domain expertise or estimated (see Section Semi-Supervised Learning ). Inserting the distribution \eqref{equ_augm_mvn_cov_matris} into \eqref{equ_def_ERM_funs_aug_approx},
Note that \eqref{equ_def_ERM_funs_aug_approx_ridge_cov} reduces to ordinary ridge regression \eqref{equ_def_ERM_funs_aug_approx_ridge} for the choice [math]\mC = \sigma^{2} \mathbf{I}[/math].
Statistical and Computational Aspects of Regularization
The goal of this section is to develop a better understanding for the effect of the regularization term in SRM \eqref{equ_rerm_weight}. We will analyze the solutions of ridge regression \eqref{equ_rerm_ridge_regression} which is the special case of SRM using the linear hypothesis space and squared squared error loss. Using the feature matrix [math]\mX\!=\!\big(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)}\big)^{T}[/math] and label vector [math]\labelvec\!=\!(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)})^{T}[/math], we can rewrite \eqref{equ_rerm_ridge_regression} more compactly as
The solution of \eqref{equ_def_rlr_w_opt} is given by
For [math]\regparam\!=\!0[/math], \eqref{equ_close_form_reglinreg} reduces to the formula for the optimal weights in linear regression (see \eqref{equ_rerm_ridge_regression} and equ_def_cost_MSE). Note that for [math]\regparam\gt0[/math], the formula \eqref{equ_close_form_reglinreg} is always valid, even when [math]\featuremtx^{T} \featuremtx[/math] is singular (not invertible). For [math]\regparam\gt 0[/math] the optimization problem \eqref{equ_def_rlr_w_opt} (and \eqref{equ_rerm_ridge_regression}) has the unique solution \eqref{equ_close_form_reglinreg}.
To study the statistical properties of the predictor [math]h^{(\widehat{\weights}^{(\regparam)})}(\featurevec) = \big(\widehat{\weights}^{(\regparam)}\big)^{T} \featurevec[/math](see \eqref{equ_close_form_reglinreg}) we use the probabilistic toy model equ_linear_obs_model, equ_toy_model_iid and equ_labels_training_data that we used already in Section A Probabilistic Analysis of Generalization . We interpret the training data [math]\dataset^{(\rm train)} = \{ (\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math] as realizations of iid RVs whose distribution is defined by equ_linear_obs_model, equ_toy_model_iid and equ_labels_training_data.
We can then define the average prediction error of ridge regression as
As shown in Section A Probabilistic Analysis of Generalization , the error [math]\error_{\rm pred}^{(\regparam)}[/math] is the sum of three components: the bias, the variance and the noise variance [math]\sigma^{2}[/math] (see equ_decomp_E_pred_toy_model). The bias of [math]\widehat{\weights}^{(\regparam)}[/math] is
For sufficiently large size [math]\samplesize[/math] of the training set, we can use the approximation
such that \eqref{equ_bias_reg_lin_reg} can be approximated as
Let us compare the (approximate) bias term \eqref{equ_bias_reg_lin_reg_approx} of ridge regression with the bias term of ordinary linear regression (which is the extreme case of ridge regression with [math]\regparam=0[/math]). The bias term \eqref{equ_bias_reg_lin_reg_approx} increases with increasing regularization parameter [math]\regparam[/math] in ridge regression \eqref{equ_rerm_ridge_regression}. Sometimes the increase in bias is outweighed by the reduction in variance. The variance typically decreases with increasing [math]\regparam[/math] as shown next.
The variance of ridge regression \eqref{equ_rerm_ridge_regression} satisfies
Inserting the approximation \eqref{equ_approx_Gram_large_N} into \eqref{equ_variance_reglinreg},
According to \eqref{equ_variance_reglinreg_approx}, the variance of [math]\widehat{\weights}^{(\regparam)}[/math] decreases with increasing regularization parameter [math]\regparam[/math] of ridge regression \eqref{equ_rerm_ridge_regression}. This is the opposite behaviour as observed for the bias \eqref{equ_bias_reg_lin_reg_approx}, which increases with increasing [math]\regparam[/math]. By comparing the variance approximation \eqref{equ_variance_reglinreg_approx} with the variance of linear regression suggests to interpret the ratio [math]\featuredim/(1\!+\!\regparam)^2[/math] as an effective number of features used by ridge regression. Increasing the regularization parameter [math]\regparam[/math] decreases the effective number of features.
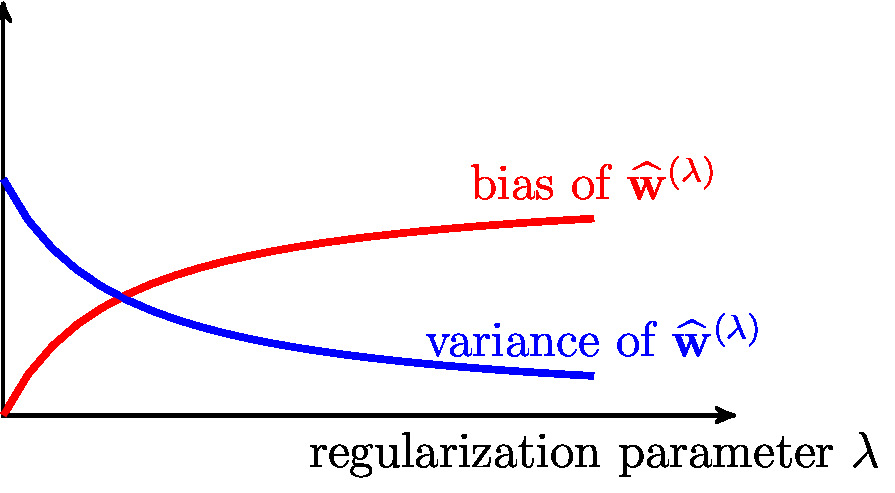
Figure fig_bias_variance_lambda illustrates the trade-off between the bias [math]\biasterm^{2}[/math] \eqref{equ_bias_reg_lin_reg_approx} of ridge regression, which increases for increasing [math]\regparam[/math], and the variance [math]\varianceterm[/math] \eqref{equ_variance_reglinreg_approx} which decreases with increasing [math]\regparam[/math]. Note that we have seen another example for a bias-variance trade-off in Section A Probabilistic Analysis of Generalization . This trade-off was traced out by a discrete (model complexity) parameter [math]\modelidx \in \{1,2,\ldots\}[/math] (see equ_generalization_hypospace_r). In stark contrast to discrete model selection, the bias-variance trade-off for ridge regression is traced out by the continuous regularization parameter [math]\regparam \in \mathbb{R}_{+}[/math].
The main statistical effect of the regularization term in ridge regression is to
balance the bias with the variance to minimize the average prediction error of
the learnt hypothesis. There is also a computational effect or adding a regularization term.
Roughly speaking, the regularization term serves as a pre-conditioning of the optimization
problem and, in turn, reduces the computational complexity of solving ridge regression \eqref{equ_def_rlr_w_opt}.
The objective function in \eqref{equ_def_rlr_w_opt} is a smooth (infinitely often differentiable) convex function. We can therefore use GD to solve \eqref{equ_def_rlr_w_opt} efficiently (see Chapter Gradient-Based Learning ). Algorithm alg:gd_reglinreg summarizes the application of GD to \eqref{equ_def_rlr_w_opt}. The computational complexity of Algorithm alg:gd_reglinreg depends crucially on the number of GD iterations required to reach a sufficiently small neighbourhood of the solutions to \eqref{equ_def_rlr_w_opt}. Adding the regularization term [math]\regparam \| \weights \|^{2}_{2}[/math] to the objective function of linear regression speeds up GD. To verify this claim, we first rewrite \eqref{equ_def_rlr_w_opt} as the quadratic problem
This is similar to the quadratic optimization problem underlying linear regression but with a different matrix [math]\mQ[/math]. The computational complexity (number of iterations) required by GD (see equ_def_GD_step) to solve \eqref{equ_quadr_form_reglinreg} up to a prescribed accuracy depends crucially on the condition number [math]\kappa(\mQ) \geq 1[/math] of the positive semi-definite (psd) matrix [math]\mQ[/math] [11]. The smaller the condition number [math]\kappa(\mQ)[/math], the fewer iterations are required by GD. We refer to a matrix with a small condition number as being “well-conditioned”.
The condition number of the matrix [math]\mQ[/math] in \eqref{equ_quadr_form_reglinreg} is given by
According to \eqref{equ_def_cond_number_ridgereg}, the condition number [math]\kappa(\mQ)[/math] tends to one for increasing regularization parameter [math]\regparam[/math],
Thus, the number of required GD iterations in Algorithm alg:gd_reglinreg decreases with increasing regularization parameter [math]\regparam[/math].
Input: dataset [math]\dataset=\{ (\featurevec^{(\sampleidx)}, \truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math]; GD learning rate [math]\lrate \gt0[/math].
- repeat
- [math]\itercntr \defeq \itercntr +1[/math] (increase iteration counter)
- [math]\weights^{(\itercntr)} \defeq (1- \lrate \regparam) \weights^{(\itercntr\!-\!1)} + \lrate (2/\samplesize) \sum_{\sampleidx=1}^{\samplesize} (\truelabel^{(\sampleidx)} - \big(\weights^{(\itercntr\!-\!1)})^{T} \featurevec^{(\sampleidx)}) \featurevec^{(\sampleidx)}[/math] (do a GD step)
- until stopping criterion met
Semi-Supervised Learning
Consider the task of predicting the numeric label [math]y[/math] of a data point [math]\vz=\big(\featurevec,y\big)[/math] based on its feature vector [math]\featurevec\!=\!\big(x_{1},\ldots,x_{\featurelen}\big)^{T} \in \mathbb{R}^{\featurelen}[/math]. At our disposal are two datasets [math]\dataset^{(u)}[/math] and [math]\dataset^{(l)}[/math]. For each datapoint in [math]\dataset^{(u)}[/math] we only know the feature vector. We therefore refer to [math]\dataset^{(u)}[/math] as “unlabelled data”. For each datapoint in [math]\dataset^{(l)}[/math] we know both, the feature vector [math]\featurevec[/math] and the label [math]y[/math]. We therefore refer to [math]\dataset^{(l)}[/math] as “labeled data”.
SSL methods exploit the information provided by unlabelled data [math]\dataset^{(u)}[/math] to support the learning of a hypothesis based on minimizing its empirical risk on the labelled (training) data [math]\dataset^{(l)}[/math]. The success of SSL methods depends on the statistical properties of the data generated within a given application domain. Loosely speaking, the information provided by the probability distribution of the features must be relevant for the ultimate task of predicting the label [math]y[/math] from the the features [math]\featurevec[/math] [1].
Let us design a SSL method, summarized in Algorithm alg:ssl_linreg below, using the data augmentation perspective from Section Data Augmentation . The idea is the augment the (small) labeled dataset [math]\dataset^{(l)}[/math] by adding random perturbations fo the features vectors of data point in [math]\dataset^{(l)}[/math]. This is reasonable for applications where feature vectors are subject to inherent measurement or modelling errors. Given a data point with vector [math]\featurevec[/math] we could have equally well observed a feature vector [math]\featurevec + {\bm \varepsilon}[/math] with some small random perturbation [math]{\bm \varepsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{C})[/math]. To estimate the covariance matrix [math]\mC[/math], we use the sample covariance matrix of the feature vectors in the (large) unlabelled dataset [math]\dataset^{(u)}[/math]. We then learn a hypothesis using the augmented (regularized) ERM \eqref{equ_def_ERM_funs_aug_approx_ridge_cov}.
Input: labeled dataset [math]\dataset^{(l)}=\{ (\featurevec^{(\sampleidx)}, y^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math]; unlabeled dataset [math]\dataset^{(u)}=\{ \widetilde{\featurevec}^{(\sampleidx)} \}_{\sampleidx=1}^{\samplesize'}[/math]
- compute [math]\mC[/math] via sample covariance on [math]\dataset^{(u)}[/math],
[[math]] \begin{equation} \mC \defeq (1/\samplesize') \sum_{\sampleidx=1}^{\samplesize'} \big(\widetilde{\featurevec}^{(\sampleidx)}\!-\!\widehat{\featurevec} \big) \big(\widetilde{\featurevec}^{(\sampleidx)}\!-\!\widehat{\featurevec} \big)^{T} \mbox{ with } \widehat{\featurevec} \defeq (1/\samplesize') \sum_{\sampleidx=1}^{\samplesize'} \widetilde{\featurevec}^{(\sampleidx)}. \end{equation} [[/math]]
- compute (e.g. using GD)
[[math]] \begin{align} \label{equ_def_ERM_funs_aug_approx_ridge_cov_weights} \widehat{\vw} \defeq \argmin_{\vw \in \mathbb{R}^{\featuredim}} \bigg[ (1/\samplesize) \sum_{\sampleidx=1}^{\samplesize} \big( y^{(\sampleidx)} - \weights^{T}\featurevec^{(\sampleidx)} \big) ^{2} + \vw^{T} \mC \vw \bigg] . \end{align} [[/math]]
Multitask Learning
Consider a specific learning task of finding a hypothesis [math]h[/math] with minimum (expected) loss [math]\loss{(\featurevec,\truelabel)}{h}[/math]. Note that the loss incurred by [math]h[/math] for a specific data point depends on the definition for the label of a data point. We can obtain different learning tasks for the same data points by using different choices or definitions for the label of a data point. Multitask learning exploits the similarities between different learning tasks to jointly solve them. Let us next discuss a simple example of a multitask learning problem.
Consider a data point [math]\vz[/math] representing a hand-drawing that is collected via the online game [1]. The features of a data point are the pixel intensities of the bitmap which is used to store the hand-drawing. As label we could use the fact if a hand-drawing shows an apple or not. This results in the learning task [math]\task^{(1)}[/math]. Another choice for the label of a hand-drawing could be the fact if a hand-drawing shows a fruit at all or not. This results in another learning task [math]\task^{(2)}[/math] which is similar but different from the task [math]\task^{(1)}[/math].
The idea of multitask learning is that a reasonable hypothesis [math]h[/math] for a learning task should also do well for a related learning tasks. Thus, we can use the loss incurred on similar learning tasks as a regularization term for learning a hypothesis for the learning task at hand. Algorithm alg:mtl is a straightforward implementation of this idea for a given dataset that gives rise to [math]\nrtasks[/math] related learning tasks [math]\task^{(1)},\ldots,\task^{(\nrtasks)}[/math]. For each individual learning task [math]\task^{(\taskidx')}[/math] it uses the loss on the remaining learning tasks [math]\task^{(\taskidx)}[/math], with [math]\taskidx \neq \taskidx'[/math], as regularization term in \eqref{equ_def_ERM_mt}.
Input: dataset [math]\dataset = \{\datapoint^{(1)},\ldots,\datapoint^{(\samplesize)} \}[/math]; [math]\nrtasks[/math] learning tasks with loss functions [math]\lossfun^{(1)},\ldots,\lossfun^{(\nrtasks)}[/math], hypothesis space [math]\hypospace[/math]
- learn a hypothesis [math]\hat{h}[/math] via
[[math]] \begin{align} \label{equ_def_ERM_mt} \hat{h} \defeq \argmin_{h \in \hypospace} \sum_{\taskidx=1}^{\nrtasks} \sum_{\sampleidx=1}^{\samplesize} \lossfun^{(\taskidx)}\big(\datapoint^{(\sampleidx)},h\big). \end{align} [[/math]]
Output: hypothesis [math]\hat{h}[/math]
The applicability of Algorithm alg:mtl is somewhat limited as it aims at finding a single hypothesis that does
well for all [math]\nrtasks[/math] learning tasks simultaneously. For certain application domains it might be more reasonable
to not learn a single hypothesis for all learning tasks but to learn a separate hypothesis [math]h^{(\taskidx)}[/math] for each
learning task [math]\taskidx=1,\ldots,\nrtasks[/math]. However, these separate hypotheses typically might still share some
structural similarities.[a]
We can enforce different notion of similarities between the hypotheses [math]h^{(\taskidx)}[/math] by adding a regularization term to the loss functions of the tasks.
Algorithm alg:mtl_reg generalizes Algorithms alg:mtl by learning a separate hypothesis for each task [math]\taskidx[/math] while requiring these hypotheses to be structurally similar. The structural (dis-)similarity between the hypotheses is measured by a regularization term [math]\regularizer[/math] in \eqref{equ_def_ERM_mt_reg}.
Input: dataset [math]\dataset = \{\datapoint^{(1)},\ldots,\datapoint^{(\samplesize)} \}[/math] with [math]\nrtasks[/math] associated learning tasks with loss functions [math]\lossfun^{(1)},\ldots,\lossfun^{(\nrtasks)}[/math], hypothesis space [math]\hypospace[/math]
- learn a hypothesis [math]\hat{h}[/math] via
[[math]] \begin{align} \label{equ_def_ERM_mt_reg} \hat{h}^{(1)},\ldots,\hat{h}^{(\nrtasks)} \defeq \argmin_{h^{(1)},\ldots,h^{(\nrtasks)} \in \hypospace} \sum_{\taskidx=1}^{\nrtasks} \sum_{\sampleidx=1}^{\samplesize} \lossfun^{(\taskidx)}\big(\vz^{(\sampleidx)},h^{(\taskidx)}\big) + \regparam \regularizer \big(h^{(1)},\ldots,h^{(\nrtasks)}\big). \end{align} [[/math]]
Transfer Learning
Regularization is also instrumental for transfer learning to capitalize on synergies between different related learning tasks [13][14]. Transfer learning is enabled by constructing regularization terms for a learning task by using the result of a previous leaning task. While multitask learning methods solve many related learning tasks simultaneously, transfer learning methods operate in a sequential fashion.
Let us illustrate the idea of transfer learning using two learning tasks which differ signifcantly in their intrinsic difficulty. Informally, we consider a learning task to be easy if we can easily gather large amounts of labeled (training) data for that task. Consider the learning task [math]\task^{(1)}[/math] of predicting whether an image shows a cat or not. For this learning task we can easily gather a large training set [math]\dataset^{(1)}[/math] using via image collections of animals. Another (related) learning task [math]\task^{(2)}[/math] is to predict whether an image shows a cat of a particular breed, with a particular body height and with a specific age. The learning task [math]\task^{(2)}[/math] is more dificult than [math]\task^{(1)}[/math] since we have only a very limited amount of cat images for which we know the particular breed, body height and precise age of the depicted cat.
Notes
- One important example for such a structural similarity in the case of linear predictors [math]h^{(\taskidx)}(\featurevec) =\big(\weights^{(\taskidx)} \big)^{T} \featurevec[/math]is that the parameter vectors [math]\vw^{(\nrtasks)}[/math] have a small joint support. Requiring the parameter vectors to have a small joint support is equivalent to requiring the stacked vector [math]\widetilde{\weights}=\big(\weights^{(1)},\ldots,\weights^{(\nrtasks)} \big) [/math] to be block (group) sparse [12].
General References

Jung, Alexander (2022). Machine Learning: The Basics. Signapore: Springer. doi:10.1007/978-981-16-8193-6.
Jung, Alexander (2022). "Machine Learning: The Basics". arXiv:1805.05052.
References
- 1.0 1.1 O. Chapelle, B. Schölkopf, and A. Zien, editors. Semi-Supervised Learning The MIT Press, Cambridge, Massachusetts, 2006
- R. Caruana. Multitask learning. Machine Learning 28(1):41--75, 1997
- M. Wainwright. High-Dimensional Statistics: A Non-Asymptotic Viewpoint Cambridge: Cambridge University Press, 2019
- 4.0 4.1 P. Bühlmann and S. van de Geer. Statistics for High-Dimensional Data Springer, New York, 2011
- S. Shalev-Shwartz and S. Ben-David. Understanding Machine Learning -- from Theory to Algorithms Cambridge University Press, 2014
- V. N. Vapnik. The Nature of Statistical Learning Theory Springer, 1999
- S. Boyd and L. Vandenberghe. Convex Optimization Cambridge Univ. Press, Cambridge, UK, 2004
- 8.0 8.1 D. P. Bertsekas. Nonlinear Programming Athena Scientific, Belmont, MA, 2nd edition, June 1999
- 9.0 9.1 9.2 T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning Springer Series in Statistics. Springer, New York, NY, USA, 2001
- 10.0 10.1 T. Hastie, R. Tibshirani, and M. Wainwright. Statistical Learning with Sparsity. The Lasso and its Generalizations CRC Press, 2015
- A. Jung. A fixed-point of view on gradient methods for big data. Frontiers in Applied Mathematics and Statistics 3, 2017
- Y. C. Eldar, P. Kuppinger, and H. Bölcskei. Block-sparse signals: Uncertainty relations and efficient recovery. IEEE Trans. Signal Processing 58(6):3042--3054, June 2010
- S. Pan and Q. Yang. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering 22(10):1345--1359, 2010
- J. Howard and S. Ruder. Universal language model fine-tuning for text classification. In Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) pages 328--339, Melbourne, Australia, July 2018. Association for Computational Linguistics