Model Validation and Selection
[math] % Generic syms \newcommand\defeq{:=} \newcommand{\Tt}[0]{\boldsymbol{\theta}} \newcommand{\XX}[0]{{\cal X}} \newcommand{\ZZ}[0]{{\cal Z}} \newcommand{\vx}[0]{{\bf x}} \newcommand{\vv}[0]{{\bf v}} \newcommand{\vu}[0]{{\bf u}} \newcommand{\vs}[0]{{\bf s}} \newcommand{\vm}[0]{{\bf m}} \newcommand{\vq}[0]{{\bf q}} \newcommand{\mX}[0]{{\bf X}} \newcommand{\mC}[0]{{\bf C}} \newcommand{\mA}[0]{{\bf A}} \newcommand{\mL}[0]{{\bf L}} \newcommand{\fscore}[0]{F_{1}} \newcommand{\sparsity}{s} \newcommand{\mW}[0]{{\bf W}} \newcommand{\mD}[0]{{\bf D}} \newcommand{\mZ}[0]{{\bf Z}} \newcommand{\vw}[0]{{\bf w}} \newcommand{\D}[0]{{\mathcal{D}}} \newcommand{\mP}{\mathbf{P}} \newcommand{\mQ}{\mathbf{Q}} \newcommand{\E}[0]{{\mathbb{E}}} \newcommand{\vy}[0]{{\bf y}} \newcommand{\va}[0]{{\bf a}} \newcommand{\vn}[0]{{\bf n}} \newcommand{\vb}[0]{{\bf b}} \newcommand{\vr}[0]{{\bf r}} \newcommand{\vz}[0]{{\bf z}} \newcommand{\N}[0]{{\mathcal{N}}} \newcommand{\vc}[0]{{\bf c}} \newcommand{\bm}{\boldsymbol} % Statistics and Probability Theory \newcommand{\errprob}{p_{\rm err}} \newcommand{\prob}[1]{p({#1})} \newcommand{\pdf}[1]{p({#1})} \def \expect {\mathbb{E} } % Machine Learning Symbols \newcommand{\biasterm}{B} \newcommand{\varianceterm}{V} \newcommand{\neighbourhood}[1]{\mathcal{N}^{(#1)}} \newcommand{\nrfolds}{k} \newcommand{\mseesterr}{E_{\rm est}} \newcommand{\bootstrapidx}{b} %\newcommand{\modeldim}{r} \newcommand{\modelidx}{l} \newcommand{\nrbootstraps}{B} \newcommand{\sampleweight}[1]{q^{(#1)}} \newcommand{\nrcategories}{K} \newcommand{\splitratio}[0]{{\rho}} \newcommand{\norm}[1]{\Vert {#1} \Vert} \newcommand{\sqeuclnorm}[1]{\big\Vert {#1} \big\Vert^{2}_{2}} \newcommand{\bmx}[0]{\begin{bmatrix}} \newcommand{\emx}[0]{\end{bmatrix}} \newcommand{\T}[0]{\text{T}} \DeclareMathOperator*{\rank}{rank} %\newcommand\defeq{:=} \newcommand\eigvecS{\hat{\mathbf{u}}} \newcommand\eigvecCov{\mathbf{u}} \newcommand\eigvecCoventry{u} \newcommand{\featuredim}{n} \newcommand{\featurelenraw}{\featuredim'} \newcommand{\featurelen}{\featuredim} \newcommand{\samplingset}{\mathcal{M}} \newcommand{\samplesize}{m} \newcommand{\sampleidx}{i} \newcommand{\nractions}{A} \newcommand{\datapoint}{\vz} \newcommand{\actionidx}{a} \newcommand{\clusteridx}{c} \newcommand{\sizehypospace}{D} \newcommand{\nrcluster}{k} \newcommand{\nrseeds}{s} \newcommand{\featureidx}{j} \newcommand{\clustermean}{{\bm \mu}} \newcommand{\clustercov}{{\bm \Sigma}} \newcommand{\target}{y} \newcommand{\error}{E} \newcommand{\augidx}{b} \newcommand{\task}{\mathcal{T}} \newcommand{\nrtasks}{T} \newcommand{\taskidx}{t} \newcommand\truelabel{y} \newcommand{\polydegree}{r} \newcommand\labelvec{\vy} \newcommand\featurevec{\vx} \newcommand\feature{x} \newcommand\predictedlabel{\hat{y}} \newcommand\dataset{\mathcal{D}} \newcommand\trainset{\dataset^{(\rm train)}} \newcommand\valset{\dataset^{(\rm val)}} \newcommand\realcoorspace[1]{\mathbb{R}^{\text{#1}}} \newcommand\effdim[1]{d_{\rm eff} \left( #1 \right)} \newcommand{\inspace}{\mathcal{X}} \newcommand{\sigmoid}{\sigma} \newcommand{\outspace}{\mathcal{Y}} \newcommand{\hypospace}{\mathcal{H}} \newcommand{\emperror}{\widehat{L}} \newcommand\risk[1]{\expect \big \{ \loss{(\featurevec,\truelabel)}{#1} \big\}} \newcommand{\featurespace}{\mathcal{X}} \newcommand{\labelspace}{\mathcal{Y}} \newcommand{\rawfeaturevec}{\mathbf{z}} \newcommand{\rawfeature}{z} \newcommand{\condent}{H} \newcommand{\explanation}{e} \newcommand{\explainset}{\mathcal{E}} \newcommand{\user}{u} \newcommand{\actfun}{\sigma} \newcommand{\noisygrad}{g} \newcommand{\reconstrmap}{r} \newcommand{\predictor}{h} \newcommand{\eigval}[1]{\lambda_{#1}} \newcommand{\regparam}{\lambda} \newcommand{\lrate}{\alpha} \newcommand{\edges}{\mathcal{E}} \newcommand{\generror}{E} \DeclareMathOperator{\supp}{supp} %\newcommand{\loss}[3]{L({#1},{#2},{#3})} \newcommand{\loss}[2]{L\big({#1},{#2}\big)} \newcommand{\clusterspread}[2]{L^{2}_{\clusteridx}\big({#1},{#2}\big)} \newcommand{\determinant}[1]{{\rm det}({#1})} \DeclareMathOperator*{\argmax}{argmax} \DeclareMathOperator*{\argmin}{argmin} \newcommand{\itercntr}{r} \newcommand{\state}{s} \newcommand{\statespace}{\mathcal{S}} \newcommand{\timeidx}{t} \newcommand{\optpolicy}{\pi_{*}} \newcommand{\appoptpolicy}{\hat{\pi}} \newcommand{\dummyidx}{j} \newcommand{\gridsizex}{K} \newcommand{\gridsizey}{L} \newcommand{\localdataset}{\mathcal{X}} \newcommand{\reward}{r} \newcommand{\cumreward}{G} \newcommand{\return}{\cumreward} \newcommand{\action}{a} \newcommand\actionset{\mathcal{A}} \newcommand{\obstacles}{\mathcal{B}} \newcommand{\valuefunc}[1]{v_{#1}} \newcommand{\gridcell}[2]{\langle #1, #2 \rangle} \newcommand{\pair}[2]{\langle #1, #2 \rangle} \newcommand{\mdp}[5]{\langle #1, #2, #3, #4, #5 \rangle} \newcommand{\actionvalue}[1]{q_{#1}} \newcommand{\transition}{\mathcal{T}} \newcommand{\policy}{\pi} \newcommand{\charger}{c} \newcommand{\itervar}{k} \newcommand{\discount}{\gamma} \newcommand{\rumba}{Rumba} \newcommand{\actionnorth}{\rm N} \newcommand{\actionsouth}{\rm S} \newcommand{\actioneast}{\rm E} \newcommand{\actionwest}{\rm W} \newcommand{\chargingstations}{\mathcal{C}} \newcommand{\basisfunc}{\phi} \newcommand{\augparam}{B} \newcommand{\valerror}{E_{v}} \newcommand{\trainerror}{E_{t}} \newcommand{\foldidx}{b} \newcommand{\testset}{\dataset^{(\rm test)} } \newcommand{\testerror}{E^{(\rm test)}} \newcommand{\nrmodels}{M} \newcommand{\benchmarkerror}{E^{(\rm ref)}} \newcommand{\lossfun}{L} \newcommand{\datacluster}[1]{\mathcal{C}^{(#1)}} \newcommand{\cluster}{\mathcal{C}} \newcommand{\bayeshypothesis}{h^{*}} \newcommand{\featuremtx}{\mX} \newcommand{\weight}{w} \newcommand{\weights}{\vw} \newcommand{\regularizer}{\mathcal{R}} \newcommand{\decreg}[1]{\mathcal{R}_{#1}} \newcommand{\naturalnumbers}{\mathbb{N}} \newcommand{\featuremapvec}{{\bf \Phi}} \newcommand{\featuremap}{\phi} \newcommand{\batchsize}{B} \newcommand{\batch}{\mathcal{B}} \newcommand{\foldsize}{B} \newcommand{\nriter}{R} [/math]
Chapter Empirical Risk Minimization discussed empirical risk minimization (ERM) as a principled approach to learning a good hypothesis out of a hypothesis space or model. ERM based methods learn a hypothesis [math]\hat{h} \in \hypospace[/math] that incurs minimum average loss on a set of labeled data points that serve as the training set. We refer to the average loss incurred by a hypothesis on the training set as the training error. The minimum average loss achieved by a hypothesis that solves the ERM might be referred to as the training error of the overall ML method. This overall ML method is defined by the choice of hypothesis space (or model) and loss function (see Chapter The Landscape of ML ).
Empirical risk minimization (ERM) is sensible only if the training error of a hypothesis is an reliable approximation for its loss incurred on data points outside the training set. Whether the training error of a hypothesis is a reliable approximation for its loss on data points outside the training set depends on both, the statistical properties of the data points generated by an ML application and on the hypothesis space used by the ML method.
ML methods often use hypothesis spaces with a large effective dimension (see Section The Model ). As an example consider linear regression (see Section Linear Regression ) with data points having a large number [math]\featuredim[/math] of features (this setting is referred to as the high-dimensional regime). The effective dimension of the linear hypothesis space, which is used by linear regression, is equal to the number [math]\featuredim[/math] of features. Modern technology allows to collect a huge number of features about individual data points which implies, in turn, that the effective dimension of equ_lin_hypospace is large. Another example of a high-dimensional hypothesis space arises in deep learning methods using a hypothesis space are constituted by all maps represented by an artificial neural network (ANN) with billions of tunable parameters.
A high-dimensional hypothesis space is very likely to contain a hypothesis that perfectly fits any given training set. Such a hypothesis achieves a very small training error but might incur a large loss when predicting the labels of a data point that is not included in training set. Thus, the (minimum) training error achieved by a hypothesis learnt by ERM can be misleading. We say that a ML method, such as linear regression using too many features, overfits the training set when it learns a hypothesis (e.g., via ERM) that has small training error but incurs much larger loss outside the training set.
Section Overfitting shows that linear regression will overfit a training set
as soon as the number of features of a data point exceeds the size of the training set.
Section Validation demonstrates how to validate a learnt hypothesis by computing its average loss on data points which are not contained in the training set.
We refer to the set of data points used to validate the learnt hypothesis as a validation set.
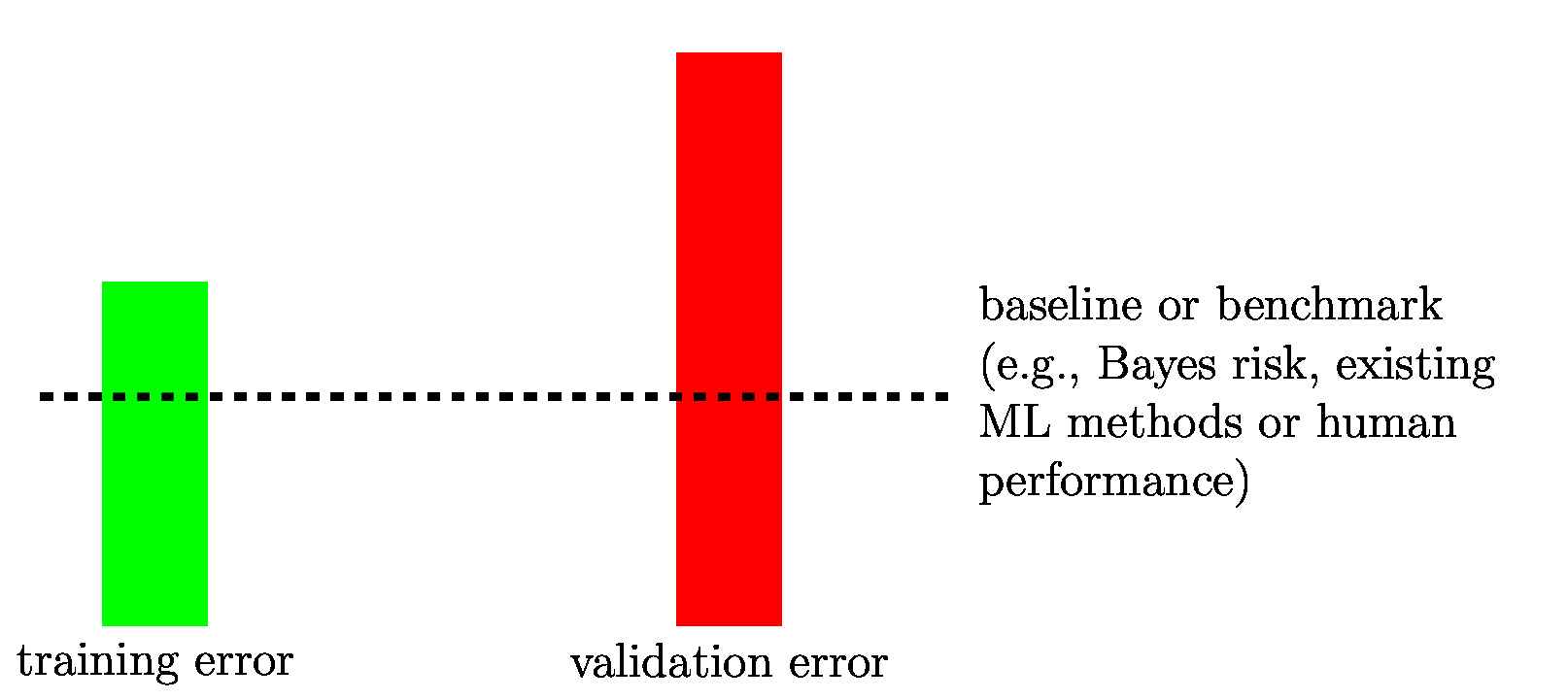
If a ML method overfits the training set, it learns a hypothesis whose training error is much smaller than its validation error. We can detect if a ML method overfits by comparing its training error with its validation error (see Figure fig_bars_val_sel).
We can use the validation error not only to detect if a ML method overfits. The validation error can also be used as a quality measure for the hypothesis space or model used by the ML method. This is analogous to the concept of a loss function that allows us to evaluate the quality of a hypothesis [math]h\!\in\!\hypospace[/math]. Section Model Selection shows how to select between ML methods using different models by comparing their validation errors.
Section A Probabilistic Analysis of Generalization uses a simple probabilistic model for the data to study the relation between the training error of a learnt hypothesis and its expected loss (see risk). This probabilistic analysis reveals the interplay between the data, the hypothesis space and the resulting training error and validation error of a ML method.
Section The Bootstrap discusses the bootstrap as a simulation based alternative to the probabilistic analysis of Section A Probabilistic Analysis of Generalization . While Section A Probabilistic Analysis of Generalization assumes a specific probability distribution of the data points, the bootstrap does not require the specification of a probability distribution underlying the data.
As indicated in Figure fig_bars_val_sel, for some ML applications, we might have a
baseline (or benchmark) for the achievable performance of ML methods. Such a baseline might be obtained from existing ML methods, human performance levels or from a probabilistic model (see Section A Probabilistic Analysis of Generalization ). Section Diagnosing ML details how the comparison between training error, validation error and (if available) a baseline
informs possible improvements for a ML method. These improvements might be obtained by collecting more data points, using more features of data points or by changing the hypothesis space (or model).
Having a baseline for the expected loss, such as the Bayes risk, allows to tell if a ML method already provides satisfactory results. If the training error and the validation error of a ML method are close to the baseline, there might be little point in trying to further improve the ML method.
Overfitting
We now have a closer look at the occurrence of overfitting in linear regression methods. As discussed in Section Linear Regression , linear regression methods learn a linear hypothesis [math]h(\featurevec) = \weights^{T} \featurevec[/math] which is parametrized by the parameter vector [math]\weights \in \mathbb{R}^{\featurelen}[/math]. The learnt hypothesis is then used to predict the numeric label [math]\truelabel \in \mathbb{R}[/math] of a data point based on its feature vector [math]\featurevec \in \mathbb{R}^{\featurelen}[/math]. Linear regression aims at finding a parameter vector [math]\widehat{\vw}[/math] with minimum average squared error loss incurred on a training set
The training set [math]\dataset[/math] consists of [math]\samplesize[/math] data points [math]\big(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}\big)[/math], for [math]\sampleidx=1,\ldots,\samplesize[/math], with known label values [math]\truelabel^{(\sampleidx)}[/math]. We stack the feature vectors [math]\featurevec^{(\sampleidx)}[/math] and labels [math]\truelabel^{(\sampleidx)}[/math], respectively, of the data points in the training set into the feature matrix [math]\featuremtx=(\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}[/math] and label vector [math]\labelvec=(\truelabel^{(1)},\ldots,\truelabel^{(\samplesize)})^{T}[/math].
The ERM of linear regression is solved by any parameter vector [math]\widehat{\weights}[/math] that solves equ_zero_gradient_lin_reg. The (minimum) training error of the hypothesis [math]h^{(\widehat{\weights})}[/math] is obtained as
Here, we used the orthogonal projection matrix [math]\mathbf{P}[/math] on the linear span
of the feature matrix [math]\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T} \in \mathbb{R}^{ \samplesize \times \featuredim}[/math].
In many ML applications we have access to a huge number of individual features to characterize a data point. As a point in case, consider a data point which is a snapshot obtained from a modern smartphone camera. These cameras have a resolution of several megapixels. Here, we can use millions of pixel colour intensities as its features. For such applications, it is common to have more features for data points than the size of the training set,
Whenever \eqref{equ_condition_overfitting} holds, the feature vectors [math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] of the data points in [math]\dataset[/math] are typically linearly independent. As a case in point, if the feature vectors
[math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] are realizations of independent and identically distributed (iid) random variable (RV)s with a continuous probability distribution, these vectors are linearly independent with probability one [1].
If the feature vectors [math]\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)} \in \mathbb{R}^{\featuredim}[/math] are linearly independent, the span of the feature matrix [math]\featuremtx = (\featurevec^{(1)},\ldots,\featurevec^{(\samplesize)})^{T}[/math] coincides with [math]\mathbb{R}^{\samplesize}[/math] which implies, in turn, [math]\mathbf{P} = \mathbf{I}[/math]. Inserting [math]\mathbf{P} = \mathbf{I}[/math] into equ_emp_risk_lin_proje yields
As soon as the number [math]\samplesize= | \dataset|[/math] of training data points does not exceed the number [math]\featuredim[/math] of features that characterize data points, there is (with probability one) a linear predictor [math]h^{(\widehat{\weights})}[/math] achieving zero training error(!).
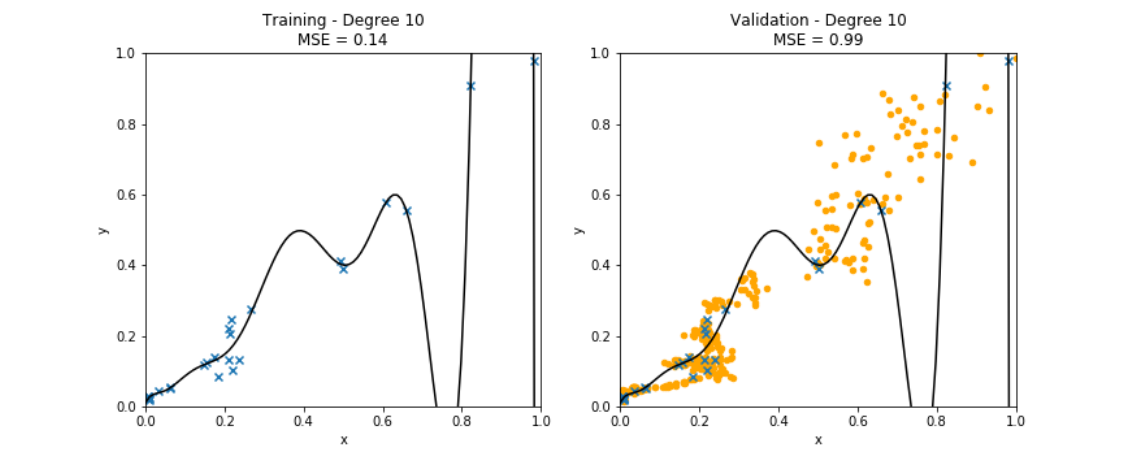
While the hypothesis [math]h^{(\widehat{\weights})}[/math] achieves zero training error, it will typically incur a non-zero average prediction error [math]\truelabel - h^{(\widehat{\weights})}(\featurevec)[/math] on data points [math](\featurevec,\truelabel)[/math] outside the training set (see Figure fig_polyn_training). Section A Probabilistic Analysis of Generalization will make this statement more precise by using a probabilistic model for the data points within and outside the training set.
Note that \eqref{eq_zero_trianing_error} also applies if the features [math]\featurevec[/math] and labels [math]y[/math] of data points are completely unrelated. Consider an ML problem with data points whose labels [math]\truelabel[/math] and features are realizations of a RV that are statistically independent. Thus, in a very strong sense, the features [math]\featurevec[/math] contain no information about the label of a data point. Nevertheless, as soon as the number of features exceeds the size of the training set, such that \eqref{equ_condition_overfitting} holds, linear regression methods will learn a hypothesis with zero training error.
We can easily extend the above discussion about the occurrence of overfitting in linear regression to other methods that combine linear regression with a feature map. Polynomial regression, using data points with a single feature [math]z[/math], combines linear regression with the feature map [math]\rawfeature \mapsto \featuremapvec(\rawfeature) \defeq \big(\rawfeature^{0},\ldots,\rawfeature^{\featurelen-1}\big)^{T}[/math] as discussed in Section Polynomial Regression .
It can be shown that whenever \eqref{equ_condition_overfitting} holds and the features
[math]\rawfeature^{(1)},\ldots,\rawfeature^{(\samplesize)}[/math] of the training set are all different, the feature vectors [math]\featurevec^{(1)}\defeq \featuremapvec \big(\rawfeature^{(1)}\big),\ldots, \featurevec^{(\samplesize)}\defeq \featuremapvec \big(\rawfeature^{(\samplesize)}\big)[/math] are linearly independent. This implies, in turn, that polynomial regression is guaranteed to find a hypothesis with zero training error whenever [math]\samplesize \leq \featurelen[/math] and the data points in the training set have different feature values.
Validation
Consider an ML method that uses ERM to learn a hypothesis [math]\hat{h} \in \hypospace[/math] out of the hypothesis space [math]\hypospace[/math]. The discussion in Section Overfitting revealed that the training error of a learnt hypothesis [math]\hat{h}[/math] can be a poor indicator for the performance of [math]\hat{h}[/math] for data points outside the training set. The hypothesis [math]\hat{h}[/math] tends to “look better” on the training set over which it has been tuned within ERM.The basic idea of validating the predictor [math]\hat{h}[/math] is simple:
- first we learn a hypothesis [math]\hat{h}[/math] using ERM on a training set and
- then we compute the average loss of [math]\hat{h}[/math] on data points that do not belong to the training set.
Thus, validation means to compute the average loss of a hypothesis using data points that have not been used in ERM to learn that hypothesis.
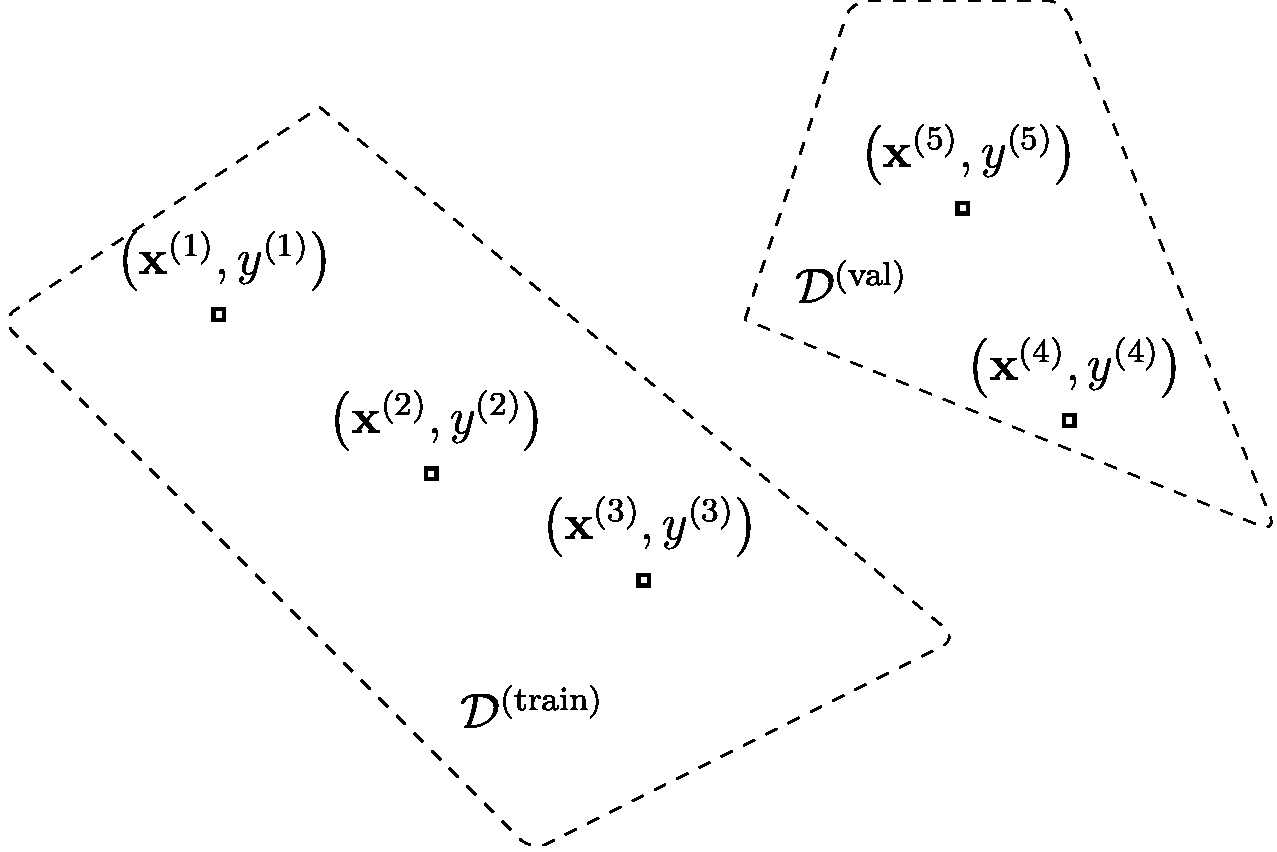
Assume we have access to a dataset of [math]\samplesize[/math] data points,
Each data point is characterized by a feature vector [math]\featurevec^{(\sampleidx)}[/math] and a label [math]\truelabel^{(\sampleidx)}[/math]. Algorithm alg:validated_ERM outlines how to learn and validate a hypothesis [math]h\in \hypospace[/math] by splitting the dataset [math]\dataset[/math] into a training set and a validation set. The random shuffling in step alg_shuffle_step of Algorithm alg:validated_ERM ensures the i.i.d. assumption for the shuffled data. Section The Size of the Validation Set shows next how the i.i.d. assumption ensures that the validation error \eqref{equ_def_training_val_val} approximates the expected loss of the hypothesis [math]\hat{h}[/math]. The hypothesis [math]\hat{h}[/math] is learnt via ERM on the training set during step equ_step_train_val_ERM of Algorithm alg:validated_ERM.
Input: model [math]\hypospace[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; split ratio [math]\splitratio[/math]
- randomly shuffle the data points in [math]\dataset[/math]
- create the training set
[math]\trainset[/math] using the first
[math]\samplesize_{t}\!=\! \lceil\splitratio \samplesize\rceil[/math] data points,
[[math]] \trainset = \big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize_{t})}, \truelabel^{(\samplesize_{t})}\big) \big\}.[[/math]]
- create the validation set
[math]\valset
[/math]
by the
[math]\samplesize_v = \samplesize - \samplesize_t[/math] remaining data points,
[[math]] \valset = \big\{ \big(\featurevec^{(\samplesize_{t}+1)}, \truelabel^{(\samplesize_{t}+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}.[[/math]]
- learn hypothesis
[math]\hat{h}
[/math]
via ERM on the training set,
[[math]] \begin{equation} \label{equ_def_hat_h_fitting} \hat{h} \defeq \argmin_{h\in \hypospace} \emperror\big(h| \trainset \big) \end{equation} [[/math]]
- compute the training error
[[math]] \begin{equation} \label{equ_def_training_error_val} \trainerror \defeq \emperror\big(\hat{h}| \trainset \big) = (1/\samplesize_{t}) \sum_{\sampleidx=1}^{\samplesize_{t}} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
- compute the validation error
[[math]] \begin{equation} \label{equ_def_training_val_val} \valerror \defeq \emperror\big(\hat{h}| \valset \big)= (1/\samplesize_{v}) \sum_{\sampleidx=\samplesize_{t}+1}^{\samplesize} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
Output: learnt hypothesis [math]\hat{h}[/math], training error [math]\trainerror[/math], validation error [math]\valerror[/math]
The Size of the Validation Set
The choice of the split ratio [math]\splitratio \approx \samplesize_{t}/ \samplesize [/math]
in Algorithm alg:validated_ERM is often based on trial and error. We try out different choices for the split ratio and pick the one with the smallest validation error. It is difficult to make a precise statement on how to choose the split ratio which applies broadly [2]. This difficulty stems from the fact that the optimal choice for [math]\rho[/math] depends on the precise statistical properties of the data points.
One approach to determine the required size of the validation set is to use a probabilistic model for the data points. The i.i.d. assumption is maybe the most widely used probabilistic model within ML. Here, we interpret data points as the realizations of iid RVs. These iid RVs have a common (joint) probability distribution
[math]p(\featurevec,\truelabel)[/math] over possible features [math]\featurevec[/math] and labels [math]\truelabel[/math] of a data point. Under the i.i.d. assumption, the validation error [math]\valerror[/math] \eqref{equ_def_training_val_val} also becomes a realization of a RV. The expectation (or mean) [math]\expect \{ \valerror \}[/math] of this RV is precisely the risk [math]\expect\{ \loss{(\featurevec,\truelabel)} {\hat{h}} \}[/math] of [math]\hat{h}[/math] (see risk).
Within the above i.i.d. assumption, the validation error [math]\valerror[/math] becomes a realization of a RV that fluctuates around its mean [math]\expect \{ \valerror \}[/math]. We can quantify this fluctuation using the variance
Note that the validation error is the average of the realizations [math]\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}[/math] of iid RVs. The probability distribution of the RV [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] is determined by the probability distribution [math]p(\featurevec,\truelabel)[/math], the choice of loss function and the hypothesis [math]\hat{h}[/math]. In general, we do not know [math]p(\featurevec,\truelabel)[/math] and, in turn, also do not know the probability distribution of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math].
If we know an upper bound [math]U[/math] on the variance of the (random) loss [math]\loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}[/math], we can bound the variance of [math]\valerror[/math] as
We can then, in turn, ensure that the variance [math]\sigma_{\valerror}^{2}[/math] of the validation error [math]\valerror[/math] does not exceed a given threshold
[math]\eta[/math], say [math]\eta = (1/100) \trainerror^2[/math], by using a validation set of size
The lower bound \eqref{equ_lower_bound_variance} is only useful if we can determine an upper bound [math]U[/math] on the variance of the RV [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] where [math]\big(\featurevec,\truelabel\big)[/math] is a RV with probability distribution [math]p(\featurevec,\truelabel)[/math]. An upper bound on the variance of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] can be derived using probability theory if we know an accurate probabilistic model [math]p(\featurevec,\truelabel)[/math] for the data points. Such a probabilistic model might be provided by application-specific scientific fields such as biology or psychology. Another option is to estimate the variance of [math]\loss{(\featurevec,\truelabel)}{\hat{h}}[/math] using the sample variance of the actual loss values [math]\loss{(\featurevec^{(1)},\truelabel^{(1)})}{\hat{h}},\ldots, \loss{(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)})}{\hat{h}}[/math] obtained for the dataset [math]\dataset[/math].
k-Fold Cross Validation
Algorithm alg:validated_ERM uses the most basic form of splitting a given dataset [math]\dataset[/math] into a training set and a validation set. Many variations and extensions of this basic splitting approach have been proposed and studied (see [3] and Section The Bootstrap ). One very popular extension of the single split into training set and validation set is known as [math]k[/math]-fold cross-validation ( [math]k[/math]-fold CV) [4](Sec. 7.10). We summarize [math]k[/math]-fold CV in Algorithm alg:kfoldCV_ERM below.
Figure fig_k_fold_CV illustrates the key principle behind [math]k[/math]-fold CV. First, we divide the entire dataset evenly into [math]\nrfolds[/math] subsets which are referred to as “folds”. The learning (via ERM) and validation of a hypothesis out of a given hypothesis space [math]\hypospace[/math] is then repeated [math]\nrfolds[/math] times.

During each repetition, we use one fold as the validation set and the remaining [math]\nrfolds-1[/math] folds as a training set. We then average the values of the training error and validation error obtained for each repetition (fold).
The average (over all [math]\nrfolds[/math] folds) validation error delivered by [math]k[/math]-fold CV tends to better estimate the expected loss or risk compared to the validation error obtained from a single split in Algorithm alg:validated_ERM. Consider a dataset that consists of a relatively small number of data points. If we use a single split of this small dataset into a training set and validation set, we might be very unlucky and choose data points for the validation set which are outliers and not representative for the statistical properties of most data points. The effect of such an unlucky split is typically averaged out when using [math]k[/math]-fold CV.
Input: model [math]\hypospace[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; number [math]\nrfolds[/math] of folds
- randomly shuffle the data points in [math]\dataset[/math]
- divide the shuffled dataset
[math]\dataset[/math] into
[math]\nrfolds[/math] folds
[math]\dataset_{1},\ldots,\dataset_{\nrfolds}[/math]
of size
[math]\foldsize=\lceil\samplesize/\nrfolds\rceil[/math],
[[math]] \begin{equation} \dataset_{1}\!=\!\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots, \big(\featurevec^{(\foldsize)}, \truelabel^{(\foldsize)}\big)\} ,\ldots,\dataset_{k}\!=\!\big\{ \big(\featurevec^{((\nrfolds\!-\!1)\foldsize+1)}, \truelabel^{((\nrfolds\!-\!1)\foldsize+1)}\big),\ldots, \big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big)\} \end{equation} [[/math]]
- For fold index [math]\foldidx=1,\ldots,\nrfolds[/math] do
- use [math]\foldidx [/math] th fold as the validation set [math]\valset=\dataset_{\foldidx}[/math]
- use rest as the training set [math]\trainset=\dataset \setminus \dataset_{\foldidx}[/math]
-
learn hypothesis
[math]\hat{h}[/math] via ERM on the training set,
[[math]] \begin{equation} \label{equ_def_hat_h_fitting_cv} \hat{h}^{(\foldidx)} \defeq \argmin_{h\in \hypospace} \emperror\big(h| \trainset \big) \end{equation} [[/math]]
- compute the training error
[[math]] \begin{equation} \label{equ_def_training_error_val_cv} \trainerror^{(\foldidx)} \defeq \emperror\big(\hat{h}| \trainset \big) = (1/\big|\trainset\big|) \sum_{\sampleidx \in \trainset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{h}. \end{equation} [[/math]]
- compute validation error
[[math]] \begin{equation} \label{equ_def_training_val_val_cv} \valerror^{(\foldidx)} \defeq \emperror\big(\hat{h}| \valset \big)= (1/\big|\valset\big|) \sum_{\sampleidx \in \valset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
- end for
-
compute average training and validation errors
[[math]] \trainerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \trainerror^{(\foldidx)}\mbox{, and }\valerror \defeq (1/\nrfolds) \sum_{\foldidx=1}^{\nrfolds} \valerror^{(\foldidx)} [[/math]]
- pick a learnt hypothesis [math]\hat{h} \defeq \hat{h}^{(\foldidx)}[/math]for some [math]\foldidx \in \{1,\ldots,\nrfolds\}[/math]
Output: learnt hypothesis [math]\hat{h}[/math]; average training error [math]\trainerror[/math]; average validation error [math]\valerror[/math]
Imbalanced Data
The simple validation approach discussed above requires the validation set to be a good representative for the overall statistical properties of the data. This might not be the case in applications with discrete valued labels and some of the label values being very rare. We might then be interested in having a good estimate of the conditional risks [math]\expect \{ \loss{(\featurevec,\truelabel)}{h} | \truelabel=\truelabel'\}[/math] where [math]\truelabel'[/math] is one of the rare label values. This is more than requiring a good estimate for the risk [math]\expect \{ \loss{(\featurevec,\truelabel)}{h} \}[/math].
Consider data points characterized by a feature vector [math]\featurevec[/math] and binary label [math]\truelabel \in \{-1,1\}[/math]. Assume we aim at learning a hypothesis [math]h(\featurevec) = \weights^{T} \featurevec[/math] to classify data points as [math]\hat{\truelabel}=1[/math] if [math]h(\featurevec) \geq 0[/math] while [math]\hat{\truelabel}=-1[/math] otherwise. The learning is based on a dataset [math]\dataset[/math] which contains only one single (!) data point with [math]\truelabel=-1[/math]. If we then split the dataset into training and validation set, it is with high probability that the validation set does not include any data point with label value [math]\truelabel=-1[/math]. This cannot happen when using [math]\nrfolds[/math]-fold CV since the single data point must be in one of the validation folds. However, even the applicability of [math]k[/math]-fold CV for such an imbalanced dataset is limited since we evaluate the performance of a hypothesis [math]h(\featurevec)[/math] using only one single data point with [math]\truelabel=-1[/math]. The resulting validation error will be dominated by the loss of [math]h(\featurevec)[/math] incurred on data points from the majority class (those with true label value [math]\truelabel=1[/math]).
To learn and validate a hypothesis with imbalanced data, it might be useful to to generate synthetic data points to enlarge the minority class. This can be done using data augmentation techniques which we discuss in Section Data Augmentation . Another option is to choose a loss function that takes the different frequencies of label values into account. Let us illustrate this approach in what follows by an illustrative example.
Consider an imbalanced dataset of size [math]\samplesize=100[/math], which contains [math]90[/math] data points with label [math]\truelabel=1[/math] but only [math]10[/math] data points with label [math]\truelabel=-1[/math]. We might want to put more weight on wrong predictions obtained for data points from the minority class (with true label value [math]\truelabel=-1[/math]). This can be done by using a much larger value for the loss [math]\loss{(\featurevec,\truelabel=-1)}{h(\featurevec)=1}[/math] than for the loss [math]\loss{(\featurevec,\truelabel=1)}{h(\featurevec)=-1}[/math] incurred by incorrectly predicting the label of a data point from the majority class (with true label value [math]\truelabel=1[/math]).
Model Selection
Chapter The Landscape of ML illustrated how many well-known ML methods are obtained by different combinations of a hypothesis space or model, loss function and data representation. While for many ML applications there is often a natural choice for the loss function and data representation, the right choice for the model is typically less obvious. We now discuss how to use the validation methods of Section Validation to choose between different candidate models.
Consider data points characterized by a single numeric feature [math]\feature\in \mathbb{R}[/math] and numeric label [math]\truelabel\in \mathbb{R}[/math]. If we suspect that the relation between feature [math]\feature[/math] and label [math]\truelabel[/math] is non-linear, we might use polynomial regression which is discussed in Section Polynomial Regression . Polynomial regression uses the hypothesis space [math]\hypospace_{\rm poly}^{(\featuredim)}[/math] with some maximum degree [math]\featuredim[/math]. Different choices for the maximum degree [math]\featuredim[/math] yield a different hypothesis space: [math]\hypospace^{(1)} = \mathcal{H}_{\rm poly}^{(0)},\hypospace^{(2)} = \mathcal{H}_{\rm poly}^{(1)},\ldots,\hypospace^{(\nrmodels)} = \hypospace_{\rm poly}^{(\nrmodels)}[/math].
Another ML method that learns non-linear hypothesis map is Gaussian basis regression (see Section Gaussian Basis Regression ). Here, different choices for the variance [math]\sigma[/math] and shifts [math]\mu[/math] of the Gaussian basis function result in different hypothesis spaces. For example, [math]\hypospace^{(1)} = \mathcal{H}^{(2)}_{\rm Gauss}[/math] with [math]\sigma=1[/math] and [math]\mu_{1}=1[/math] and [math]\mu_{2}=2[/math], [math]\hypospace^{(2)} = \hypospace^{(2)}_{\rm Gauss}[/math] with [math]\sigma = 1/10[/math], [math]\mu_{1}=10[/math], [math]\mu_{2}= 20[/math].
Algorithm alg:model_selection summarizes a simple method to choose between different candidate models [math]\hypospace^{(1)},\hypospace^{(2)},\ldots,\hypospace^{(\nrmodels)}[/math]. The idea is to first learn and validate a hypothesis [math]\hat{h}^{(\modelidx)}[/math] separately for each model [math]\hypospace^{(\modelidx)}[/math] using Algorithm alg:kfoldCV_ERM. For each model [math]\hypospace^{(\modelidx)}[/math], we learn the hypothesis
[math]\hat{h}^{(\modelidx)}[/math] via ERM \eqref{equ_def_hat_h_fitting} and then compute its validation error
[math]\valerror^{(\modelidx)}[/math] \eqref{equ_def_training_val_val}. We then choose the hypothesis [math]\hat{h}^{(\hat{\modelidx})}[/math] from those model [math]\hypospace^{(\hat{\modelidx})}[/math] which resulted in the smallest validation error [math]\valerror^{(\hat{\modelidx})} = \min_{\modelidx=1,\ldots,\nrmodels} \valerror^{(\modelidx)}[/math].
The workflow of Algorithm alg:model_selection is similar to the workflow of ERM. Remember that the idea of ERM is to learn a hypothesis out of a set of different candidates (the hypothesis space). The quality of a particular hypothesis [math]h[/math] is measured using the (average) loss incurred on some training set. We use the same principle for model selection but on a higher level. Instead of learning a hypothesis within a hypothesis space, we choose (or learn) a hypothesis space within a set of candidate hypothesis spaces. The quality of a given hypothesis space is measured by the validation error \eqref{equ_def_training_val_val}. To determine the validation error of a hypothesis space, we first learn the hypothesis [math]\hat{h} \in \hypospace[/math] via ERM \eqref{equ_def_hat_h_fitting} on the training set. Then, we obtain the validation error as the average loss of [math]\hat{h}[/math] on the validation set.
The final hypothesis [math]\hat{h}[/math] delivered by the model selection Algorithm alg:model_selection not only depends on the training set used in ERM (see \eqref{equ_def_hat_h_fitting_cv}). This hypothesis [math]\hat{h}[/math] has also been chosen based on its validation error which is the average loss on the validation set in \eqref{equ_def_training_val_val_cv}. Indeed, we compared this validation error with the validation errors of other models to pick the model [math]\hypospace^{(\hat{\modelidx})}[/math] (see step step_pick_optimal_model) which contains [math]\hat{h}[/math]. Since we used the validation error \eqref{equ_def_training_val_val_cv} of [math]\hat{h}[/math] to learn it, we cannot use this validation error as a good indicator for the general performance of [math]\hat{h}[/math].
To estimate the general performance of the final hypothesis [math]\hat{h}[/math] delivered by Algorithm alg:model_selection we must try it out on a test set. The test set, which is constructed in step equ_construct_test_set_algmodsel of Algorithm alg:model_selection, consists of data points that are neither contained in the training set \eqref{equ_def_hat_h_fitting_cv} nor the validation set \eqref{equ_def_training_val_val_cv} used for training and validating the candidate models [math]\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}[/math]. The average loss of the final hypothesis on the test set is referred to as the test error. The test error is computed in the step step_compute_test_error_mod_selection of Algorithm alg:model_selection.
Input: list of candidate models [math]\hypospace^{(1)},\ldots,\hypospace^{(\nrmodels)}[/math], loss function [math]\lossfun[/math], dataset [math]\dataset=\big\{ \big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[/math]; number [math]\nrfolds[/math] of folds, test set fraction [math]\rho[/math]
- randomly shuffle the data points in [math]\dataset[/math]
- determine size [math]\samplesize' \defeq \lceil \rho \samplesize \rceil[/math] of test set
- construct a test set
[[math]] \testset= \big\{\big(\featurevec^{(1)}, \truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize')}, \truelabel^{(\samplesize')}\big) \big\}[[/math]]
- construct a training set and a validation set,
[[math]]\dataset^{(\rm trainval)} = \big\{\big(\featurevec^{(\samplesize'+1)}, \truelabel^{(\samplesize'+1)}\big),\ldots,\big(\featurevec^{(\samplesize)}, \truelabel^{(\samplesize)}\big) \big\}[[/math]]
- For [math] \modelidx=1,\ldots,\nrmodels[/math] do
- run Algorithm alg:kfoldCV_ERM using [math]\hypospace=\hypospace^{(\modelidx)}[/math], dataset [math]\dataset=\dataset^{(\rm trainval)}[/math], loss function [math]\lossfun [/math] and [math]\nrfolds[/math] folds
- Algorithm alg:kfoldCV_ERM delivers hypothesis [math]\hat{h}[/math] and validation error [math]\valerror[/math]
- store learnt hypothesis [math]\hat{h}^{(\modelidx)}\defeq\hat{h}[/math] and validation error [math]\valerror^{(\modelidx)}\defeq\valerror[/math]
- end for
- pick model [math]\hypospace^{(\hat{\modelidx})}[/math] with minimum validation error [math]\valerror^{(\hat{\modelidx})}\!=\!\min_{\modelidx=1,\ldots,\nrmodels}\valerror^{(\modelidx)}[/math] \label{step_pick_optimal_model}
- define optimal hypothesis [math]\hat{h}= \hat{h}^{(\hat{\modelidx})}[/math]
- compute test error
[[math]] \begin{equation} \label{equ_def_training_error_val_test} \testerror \defeq \emperror\big(\hat{h}| \testset \big) = (1/\big|\testset\big|) \sum_{\sampleidx \in \testset} \loss{(\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)})}{\hat{h}}. \end{equation} [[/math]]
Sometimes it is beneficial to use different loss functions for the training and the validation of a hypothesis.
As an example, consider logistic regression and the support vector machine (SVM) which have been discussed in Sections Logistic Regression and
Support Vector Machines , respectively. Both methods use the same model which is the space of linear hypothesis maps [math]h(\featurevec) = \weights^{T} \featurevec[/math]. The main difference between these two methods is in their choice for the loss function. Logistic regression minimizes the (average) logistic losson the training set to learn the hypothesis [math]h^{(1)}(\featurevec)= \big( \weights^{(1)} \big)^{T} \featurevec
[/math]
with a parameter vector [math]\weights^{(1)}[/math]. The SVM instead minimizes the (average) hinge loss on the training set to learn the hypothesis [math]h^{(2)}(\featurevec) = \big( \weights^{(2)} \big)^{T} \featurevec[/math] with a parameter vector [math]\weights^{(2)}[/math]. It is inconvenient to compare the usefulness of the two hypotheses [math]h^{(1)}(\featurevec)[/math] and [math]h^{(2)}(\featurevec)[/math] using different loss functions to compute their validation errors. This comparison is more convenient if we instead compute the validation errors for [math]h^{(1)}(\featurevec)[/math] and [math]h^{(2)}(\featurevec)[/math] using the average 0/1 loss.
Algorithm alg:model_selection requires as one of its inputs a given list of candidate models. The longer this list, the more computation is required from Algorithm alg:model_selection. Sometimes it is possible to prune the list of candidate models by removing models that are very unlikely to have minimum validation error.
Consider polynomial regression which uses as the model the space [math]\hypospace_{\rm poly}^{(r)}[/math] of polynomials with maximum degree [math]\polydegree[/math] (see equ_def_poly_hyposapce). For [math]\polydegree=1[/math],
[math]\hypospace_{\rm poly}^{(\polydegree)}[/math] is the space of polynomials with maximum degree one (which are linear maps), [math]h(\feature)=\weight_{2}\feature+\weight_{1}[/math]. For [math]\polydegree=2[/math], [math]\hypospace_{\rm poly}^{(\polydegree)}[/math] is the space of polynomials with maximum degree two, [math]h(\feature)=\weight_{3}\feature^2 +\weight_{2}\feature+\weight_{1}.[/math] The polynomial degree [math]\polydegree[/math] parametrizes a nested set of models,
For each degree [math]\polydegree[/math], we learn a hypothesis [math]h^{(r)} \in \hypospace_{\rm poly}^{(\polydegree)}[/math] with minimum average loss (training error) [math]\trainerror^{(\polydegree)}[/math] on a training set (see \eqref{equ_def_training_error_val}). To validate the learnt hypothesis [math]h^{(\polydegree)}[/math], we compute its average loss (validation error) [math]\valerror^{(\polydegree)}[/math] on a validation set (see \eqref{equ_def_training_val_val}).
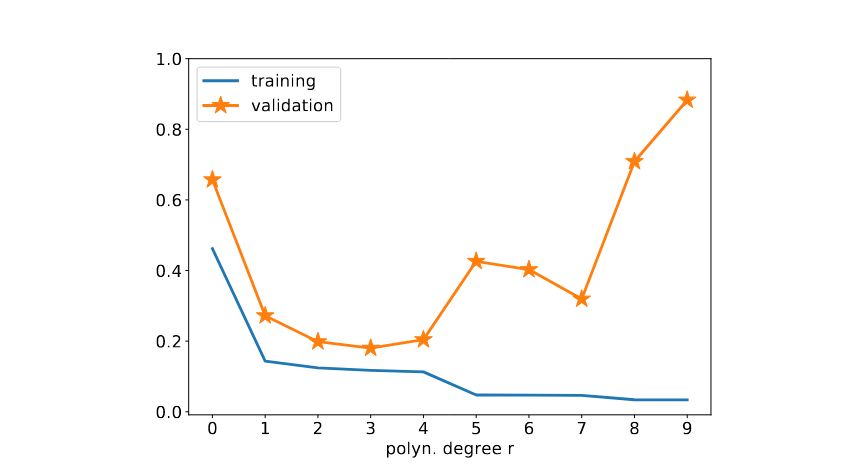
Figure fig_trainvalvsdegree depicts the typical dependency of the training and validation errors on the polynomial degree [math]\polydegree[/math]. The training error [math]\trainerror^{(\polydegree)}[/math] decreases monotonically with increasing polynomial degree [math]\polydegree[/math]. To illustrate this monotonic decrease, we consider the two specific choices [math]\polydegree=3[/math] and [math]\polydegree=5[/math] with corresponding models [math]\hypospace^{(\polydegree)}_{\rm poly}[/math] and [math]\hypospace^{(\polydegree)}_{\rm poly}[/math]. Note that [math]\hypospace^{(3)}_{\rm poly} \subset \hypospace^{(5)}_{\rm poly}[/math] since any polynomial with degree not exceeding [math]3[/math] is also a polynomial with degree not exceeding [math]5[/math]. Therefore, the training error \eqref{equ_def_training_error_val} obtained when minimizing over the larger model [math] \hypospace^{(5)}_{\rm poly}[/math] can only decrease but never increase compared to \eqref{equ_def_training_error_val} using the smaller model [math] \hypospace^{(3)}_{\rm poly}[/math] Figure fig_trainvalvsdegree indicates that the validation error [math]\valerror^{(\polydegree)}[/math] (see \eqref{equ_def_training_val_val}) behaves very different compared to the training error [math]\trainerror^{(\polydegree)}[/math]. Starting with degree [math]\polydegree=0[/math], the validation error first decreases with increasing degree [math]\polydegree[/math]. As soon as the degree [math]\polydegree[/math] is increased beyond a critical value, the validation error starts to increase with increasing [math]\polydegree[/math]. For very large values of [math]\polydegree[/math], the training error becomes almost negligible while the validation error becomes very large. In this regime, polynomial regression overfits the training set.
Figure fig_polyregdegree9 illustrates the overfitting of polynomial regression when using a maximum degree that is too large. In particular, Figure fig_polyregdegree9 depicts a learnt hypothesis which is a degree [math]9[/math] polynomial that fits very well the training set, resulting in a very small training error. To achieve this low training error the resulting polynomial has an unreasonable high rate of change for feature values [math]\feature \approx 0[/math]. This results in large prediction errors for data points with feature values [math]x \approx 0[/math].
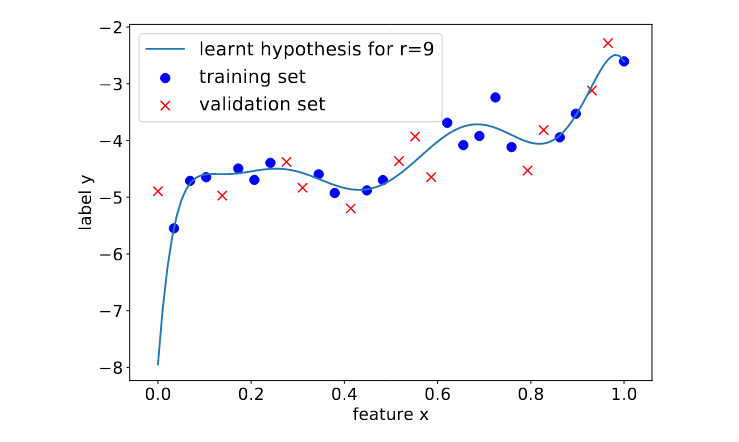
A Probabilistic Analysis of Generalization
More Data Beats Clever Algorithms ?; More Data Beats Clever Feature Selection?
A key challenge in ML is to ensure that a hypothesis that predicts well the labels on a training set (which has been used to learn that hypothesis) will also predict well the labels of data points outside the training set. We say that a ML method generalizes well if it learns a hypothesis [math]\hat{h}[/math] that performs not significantly worse on data points outside the training set. In other words, the loss incurred by [math]\hat{h}[/math] for data points outside the training set is not much larger than the average loss of [math]\hat{h}[/math] incurred on the training set.
We now study the generalization of linear regression methods (see Section Linear Regression ) using an i.i.d. assumption. In particular, we interpret data points as iid realizations of RVs that have the same distribution as a random data point [math]\datapoint=(\featurevec,\truelabel)[/math]. The feature vector [math]\featurevec[/math] is then a realization of a standard Gaussian RV with zero mean and covariance being the identity matrix, i.e., [math]\featurevec \sim \mathcal{N}(\mathbf{0}, \mathbf{I})[/math].
The label [math]\truelabel[/math] of a random data point is related to its features [math]\featurevec[/math] via a linear Gaussian model
We assume the noise variance [math]\sigma^{2}[/math] fixed and known. This is a simplifying assumption and in practice we would need to estimate the noise variance from data [5]. Note that, within our probabilistic model, the error component [math]\varepsilon[/math] in \eqref{equ_linear_obs_model} is intrinsic to the data and cannot be overcome by any ML method. We highlight that the probabilistic model for the observed data points is just a modelling assumption. This assumption allows us to study some fundamental behaviour of ML methods. There are principled methods (“statistical tests”) that allow to determine if a given dataset can be accurately modelled using \eqref{equ_linear_obs_model} [6].
We predict the label [math]\truelabel[/math] from the features [math]\featurevec[/math] using a linear hypothesis [math]h(\featurevec)[/math] that depends only on the first [math]\modelidx[/math] features [math]\feature_{1},\ldots,\feature_{\modelidx}[/math]. Thus, we use the hypothesis space
Note that each element [math]h^{(\weights)} \in \hypospace^{(\modelidx)}[/math] corresponds to a particular choice of the parameter vector [math]\weights \in \mathbb{R}^{\modelidx}[/math].
The model parameter [math]\modelidx \in \{0,\ldots,\featuredim\}[/math] coincides with the effective dimension of the hypothesis space [math]\hypospace^{(\modelidx)}[/math]. For [math]\modelidx\lt \featuredim[/math], the hypothesis space [math]\hypospace^{(\modelidx)}[/math] is a proper (strict) subset of the space of linear hypothesis maps used within linear regression (see Section Linear Regression ). Moreover, the parameter [math]\modelidx[/math] indexes a nested sequence of models,
The quality of a particular predictor [math]h^{(\weights)} \in \hypospace^{(\modelidx)}[/math] is measured via the average squared error [math]\emperror (h^{(\weights)} \mid \trainset)[/math] incurred on the labeled training set
We interpret data points in the training set [math]\trainset[/math] as well as any other data point outside the training set as realizations of iid RVs with a common probability distribution. This common probability distribution is a multivariate normal (Gaussian) distribution,
The labels [math]\truelabel^{(\sampleidx)},\truelabel[/math] are related to the features of data points via (see \eqref{equ_linear_obs_model})
Here, the noise terms [math]\varepsilon, \varepsilon^{(\sampleidx)} \sim \mathcal{N}(0,\sigma^{2})[/math] are realizations of iid Gaussian RVs with zero mean and variance [math]\sigma^{2}[/math].
Chapter Empirical Risk Minimization showed that the training error [math]\emperror (h^{(\weights)} \mid \trainset)[/math] is minimized by the predictor [math]h^{(\widehat{\weights})}(\featurevec) = \widehat{\weights}^{T} \mathbf{I}_{\modelidx \times \featuredim} \featurevec[/math], that uses the parameter vector
Here we used the (restricted) feature matrix [math]\mX^{(\modelidx)}[/math] and the label vector [math]\labelvec[/math] defined as, respectively,
It will be convenient to tolerate a slight abuse of notation and denote both, the length- [math]\modelidx[/math] vector \eqref{equ_optimal_weight_closed_form} as well as the zero-padded parameter vector [math]\big(\widehat{\weights}^{T},\mathbf{0}^{T}\big)^{T} \in \mathbb{R}^{\featuredim}[/math], by [math]\widehat{\weights}[/math]. This allows us to write
We highlight that the formula \eqref{equ_optimal_weight_closed_form} for the optimal weight vector [math]\widehat{\weights}[/math] is only valid if the matrix [math]\big(\featuremtx^{(\modelidx)}\big)^{T} \featuremtx^{(\modelidx)}[/math] is invertible. Within our toy model (see \eqref{equ_toy_model_iid}), this is true with probability one whenever [math]\samplesize_{\rm t} \geq \modelidx[/math]. Indeed, for [math]\samplesize_{\rm t} \geq \modelidx[/math] the truncated feature vectors [math]\mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(1)}, \ldots, \mathbf{I}_{\modelidx \times \featuredim} \featurevec^{(\samplesize_{t})}[/math], which are iid realizations of a Gaussian RV, are linearly independent with probability one [7][8].
In what follows, we consider the case [math]\samplesize_{\rm t} \gt \modelidx[/math] such that the formula \eqref{equ_optimal_weight_closed_form} is valid (with probability one). The more challenging high-dimensional regime [math]\samplesize_{\rm t} \leq \modelidx[/math] will be studied in Chapter Regularization .
The optimal parameter vector [math]\widehat{\weights}[/math] (see \eqref{equ_optimal_weight_closed_form}) depends on the training set [math]\trainset[/math] via the feature matrix [math]\featuremtx^{(\modelidx)}[/math] and label vector [math]\labelvec[/math] (see \eqref{equ_def_feature_matrix_r}). Therefore, since we model the data points in the training set as realizations of RVs, the parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form} is the realization of a RV. For each specific realization of the training set [math]\trainset[/math], we obtain a specific realization of the optimal parameter vector [math]\widehat{\weights}[/math].
The probabilistic model \eqref{equ_linear_obs_model} relates the features [math]\featurevec[/math] of a data point to its label [math]\truelabel[/math] via some (unknown) true parameter vector [math]\overline{\weights}[/math]. Intuitively, the best linear hypothesis would be [math]h(\featurevec) =\widehat{\weights}^{T} \featurevec[/math] with parameter vector [math]\widehat{\weights} = \overline{\weights}[/math]. However, in general this will not be achievable since we have to compute [math]\widehat{\weights}[/math] based on the features [math]\featurevec^{(\sampleidx)}[/math] and noisy labels [math]\truelabel^{(\sampleidx)}[/math] of the data points in the training set [math]\dataset[/math].
The parameter vector [math]\widehat{\vw}[/math] delivered by ERM typically results in a non-zero estimation error
The estimation error \eqref{equ_def_est_error} is the realization of a RV since the learnt parameter vector [math]\widehat{\weights}[/math] (see \eqref{equ_optimal_weight_closed_form}) is itself a realization of a RV.
The Bias and Variance Decomposition. The prediction accuracy of [math]h^{(\widehat{\weights})}[/math], using the learnt parameter vector \eqref{equ_optimal_weight_closed_form}, depends crucially on the mean squared estimation error (MSEE)
We will next decompose the MSEE [math]\mseesterr[/math] into two components, which are referred to as a variance term and a bias term. The variance term quantifies the random fluctuations or the parameter vector obtained from ERM on the training set \eqref{equ_def_train_set_prob_analysis_generatlization}. The bias term characterizes the systematic (or expected) deviation between the true parameter vector [math]\overline{\weights}[/math] (see \eqref{equ_linear_obs_model}) and the (expectation of the) learnt parameter vector [math]\widehat{\weights}[/math].
Let us start with rewriting \eqref{equ_def_est_err} using elementary manipulations as
We can develop the last expression further by expanding the squared Euclidean norm,
The first component in \eqref{equ_bias_var_decomp} represents the (expected) variance of the learnt parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form}. Note that, within our probabilistic model, the training set \eqref{equ_def_train_set_prob_analysis_generatlization} is the realization of a RV since it is constituted by data points that are iid realizations of RVs (see \eqref{equ_toy_model_iid} and \eqref{equ_linear_obs_model}).
The second component in \eqref{equ_bias_var_decomp} is referred to as a bias term. The parameter vector [math]\widehat{\weights}[/math] is computed from a randomly fluctuating training set via \eqref{equ_optimal_weight_closed_form} and is therefore itself fluctuating around its expectation [math]\expect \big \{\widehat{\weights}\}[/math]. The bias term is the Euclidean distance between this expectation [math]\expect \big \{\widehat{\weights}\}[/math] and the true parameter vector [math]\overline{\weights}[/math] relating features and label of a data point via \eqref{equ_linear_obs_model}.
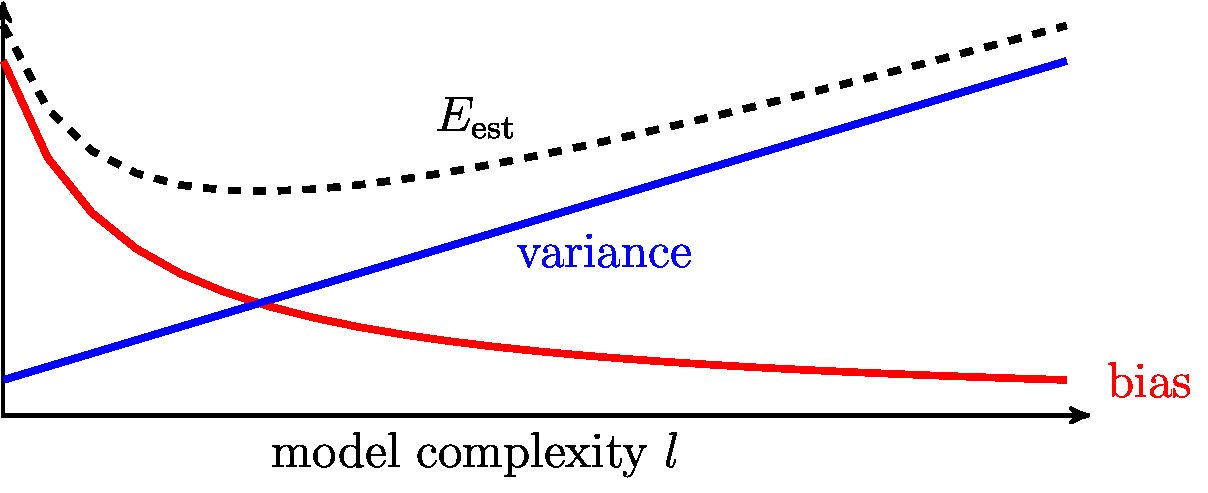
The bias term [math]\biasterm^{2}[/math] and the variance [math]\varianceterm[/math] in \eqref{equ_bias_var_decomp} both depend on the model complexity parameter [math]\modelidx[/math] but in a fundamentally different manner. The bias term [math]\biasterm^{2}[/math] typically decreases with increasing [math]\modelidx[/math] while the variance [math]\varianceterm[/math] increases with increasing [math]\modelidx[/math]. In particular, the bias term is given as
The bias term \eqref{equ_def_bias_term} is zero if and only if
The necessary and sufficient condition \eqref{equ_def_zero_bias_weght_elements} for zero bias is equivalent to [math]h^{(\overline{\weights})} \in \hypospace^{(\modelidx)}[/math]. Note that the condition \eqref{equ_def_zero_bias_weght_elements} depends on both, the model parameter [math]\modelidx[/math] and the true parameter vector [math]\overline{\weights}[/math]. While the model parameter [math]\modelidx[/math] is under control, the true parameter vector [math]\overline{\weights}[/math] is not under our control but determined by the underlying data generation process. The only way to ensure \eqref{equ_def_zero_bias_weght_elements} for every possible parameter vector [math]\overline{\weights}[/math] in \eqref{equ_linear_obs_model} is to use [math]\modelidx=\featuredim[/math], i.e., to use all available features [math]\feature_{1},\ldots,\feature_{\featuredim}[/math] of a data point.
When using the model [math]\hypospace^{(\modelidx)}[/math] with [math]\modelidx \lt \featuredim[/math], we cannot guarantee a zero bias term since we have no control over the true underlying parameter vector [math]\overline{\weights}[/math] in \eqref{equ_linear_obs_model}. In general, the bias term decreases with an increasing model size [math]\modelidx[/math] (see Figure fig_bias_variance). We highlight that the bias term does not depend on the variance [math]\sigma^{2}[/math] of the noise [math]\varepsilon[/math] in our toy model \eqref{equ_linear_obs_model}.
Let us now consider the variance term in \eqref{equ_bias_var_decomp}. Using the statistical independence of the features and labels of data points (see \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}), one can show that [a]
By \eqref{equ_toy_model_iid}, the matrix [math]\left(\big(\featuremtx^{(\modelidx)}\big)^{T} \mX^{(\modelidx)} \right)^{-1}[/math] is a realization of a (matrix-valued) RV with an inverse Wishart distribution [10]. For [math]\samplesize_{\rm t} \gt \modelidx+1[/math], its expectation is given as
By inserting \eqref{equ_expr_expect_inv-wishart} and [math]\mbox{tr} \{ \mathbf{I} \} = \modelidx[/math] into \eqref{equ_variance_term_toy_model},
The variance \eqref{equ_formulae_variance_toy_model} typically increases with increasing model complexity [math]\modelidx[/math] (see Figure fig_bias_variance). In contrast, the bias term \eqref{equ_def_bias_term} decreases with increasing [math]\modelidx[/math].
The opposite dependence of variance and bias on the model complexity results in a bias-variance trade-off. Choosing a model (hypothesis space) with small bias will typically result in large variance and vice versa. In general, the choice of model must balance between a small variance and a small bias.
Generalization.
Consider a linear regression method that learns the linear hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] using the parameter vector \eqref{equ_optimal_weight_closed_form}. The parameter vector [math]\widehat{\weights}^{T}[/math] \eqref{equ_optimal_weight_closed_form} results in a linear hypothesis with minimum training error, i.e., minimum average loss on the training set. However, the ultimate goal of ML is to find a hypothesis that predicts well the label of any data point. In particular, we want the hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] to generalize well to data points outside the training set.
We quantify the generalization capability of [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] by its expected prediction loss
Note that [math]\error_{\rm pred}[/math] is a measure for the performance of a ML method and not of a specific hypothesis. Indeed, the learnt parameter vector [math]\widehat{\weights}[/math] is not fixed but depends on the data points in the training set. These data points are modelled as realizations of iid RVs and, in turn, the learnt parameter vector [math]\widehat{\weights}[/math] becomes a realization of a RV. Thus, in some sense, the expected prediction loss \eqref{equ_def_expected_pred_loss} characterizes the overall ML method that reads in a training set and delivers (learn) a linear hypothesis with parameter vector [math]\widehat{\weights}[/math] \eqref{equ_optimal_weight_closed_form}. In contrast, the risk introduced in Chapter Empirical Risk Minimization characterizes the performance of a specific (fixed) hypothesis [math]h[/math] without taking into account a learning process that delivered [math]h[/math] based on data.
Let us now relate the expected prediction loss \eqref{equ_def_expected_pred_loss} of the linear hypothesis [math]h(\featurevec) = \widehat{\weights}^{T} \featurevec[/math] to the bias and variance of \eqref{equ_optimal_weight_closed_form},
Here, step (a) uses the law of iterated expectation (see, e.g., [7]). Step (b) uses that the feature vector [math]\featurevec[/math] of a “new” data point is a realization of a RV which is statistically independent of the data points in the training set [math]\trainset[/math]. We also used our assumption that [math]\featurevec[/math] is the realization of a RV with zero mean and covariance matrix [math]\expect \{ \featurevec \featurevec^{T}\}=\mathbf{I}[/math] (see \eqref{equ_toy_model_iid}).
According to \eqref{equ_decomp_E_pred_toy_model}, the average (expected) prediction error [math]\error_{\rm pred}[/math] is the sum of three components: (i) the bias [math]\biasterm^{2}[/math], (ii) the variance [math]\varianceterm[/math] and (iii) the noise variance [math]\sigma^{2}[/math]. Figure fig_bias_variance illustrates the typical dependency of the bias and variance on the model \eqref{equ_generalization_hypospace_r}, which is parametrized by the model complexity [math]\modelidx[/math]. Note that the model complexity parameter [math]\modelidx[/math] in \eqref{equ_generalization_hypospace_r} coincides with the effective model dimension [math]\effdim{\hypospace^{(\modelidx)}}[/math] (see Section The Model ).
The bias and variance, whose sum is the estimation error [math]\error_{\rm est}[/math], can be influenced by varying the model complexity [math]\modelidx[/math] which is a design parameter. The noise variance [math]\sigma^{2}[/math] is the intrinsic accuracy limit of our toy model \eqref{equ_linear_obs_model} and is not under the control of the ML engineer. It is impossible for any ML method (no matter how computationally expensive) to achieve, on average, a prediction error smaller than the noise variance [math]\sigma^{2}[/math]. Carefully note that this statement only applies if the data points arising in a ML application can be (reasonably well) modelled as realizations of iid RVs.
We highlight that our statistical analysis, resulting the formulas for bias \eqref{equ_def_bias_term}, variance \eqref{equ_formulae_variance_toy_model} and the average prediction error \eqref{equ_decomp_E_pred_toy_model}, applies only if the observed data points can be well modelled using the probabilistic model specified by \eqref{equ_linear_obs_model}, \eqref{equ_toy_model_iid} and \eqref{equ_labels_training_data}. The validity of this probabilistic model can to be verified by principled statistical model validation techniques [11][12]. Section The Bootstrap discusses a fundamentally different approach to analyzing the statistical properties of a ML method. Instead of a probabilistic model, this approach uses random sampling techniques to synthesize iid copies of given (small) data points. We can approximate the expectation of some relevant quantity, such as the loss [math]\loss{\big(\featurevec,\truelabel \big) }{h}[/math], using an average over synthetic data [4].
The qualitative behaviour of estimation error in Figure fig_bias_variance depends on the definition for the model complexity. Our concept of effective dimension (see Section The Model ) coincides with most other notions of model complexity for the linear hypothesis space \eqref{equ_generalization_hypospace_r}. However, for more complicated models such as deep nets it is often not obvious how effective dimension is related to more tangible quantities such as total number of tunable weights or the number of artificial neurons. Indeed, the effective dimension might also depend on the specific learning algorithm such as stochastic gradient descent (SGD). Therefore, for deep nets, if we would plot estimation error against number of tunable weights we might observe a behaviour of estimation error fundamentally different from the shape in Figure fig_bias_variance. One example for such un-intuitive behaviour is known as “double descent phenomena” [13].
The Bootstrap
basic idea of bootstrap: use histogram of dataset as the underlying probability distribution; generate new data points by random sampling (with replacement) from that distribution.
Consider learning a hypothesis [math]\hat{h} \in \hypospace[/math] by minimizing the average loss incurred on a dataset [math]\dataset=\{ \big(\featurevec^{(1)},\truelabel^{(1)}\big),\ldots,\big(\featurevec^{(\samplesize)},\truelabel^{(\samplesize)}\big)\}[/math]. The data points [math]\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)[/math] are modelled as realizations of iid RVs. Let use denote the (common) probability distribution of these RVs by [math]p(\featurevec,\truelabel)[/math].
If we interpret the data points [math]\big(\featurevec^{(\sampleidx))},\truelabel^{(\sampleidx)}\big)[/math] as realizations of RVs, also the learnt hypothesis [math]\hat{h}[/math] is a realization of a RV. Indeed, the hypothesis [math]\hat{h}[/math] is obtained by solving an optimization problem that involves realizations of RVs. The bootstrap is a method for estimating (parameters of) the probability distribution [math]p(\hat{h})[/math] [4].
Section A Probabilistic Analysis of Generalization used a probabilistic model for data points to derive (the parameters of) the probability distribution [math]p(\hat{h})[/math]. Note that the analysis in Section A Probabilistic Analysis of Generalization only applies to the specific probabilistic model \eqref{equ_toy_model_iid}, \eqref{equ_labels_training_data}. In contrast, the bootstrap can be used for data points drawn from an arbitrary probability distribution.
The core idea behind the bootstrap is to use the histogram [math]\hat{p}(\datapoint)[/math] of the data points in [math]\dataset[/math] to generate [math]\nrbootstraps[/math] new datasets [math]\dataset^{(1)},\ldots,\dataset^{(\nrbootstraps)}[/math]. Each dataset is constructed such that is has the same size as the original dataset [math]\dataset[/math]. For each dataset [math]\dataset^{(\bootstrapidx)}[/math], we solve a separate ERM to obtain the hypothesis [math]\hat{h}^{(\bootstrapidx)}[/math]. The hypothesis [math]\hat{h}^{(\bootstrapidx)}[/math] is a realization of a RV whose distribution is determined by the histogram [math]\hat{p}(\datapoint)[/math] as well as the hypothesis space and the loss function used in the ERM.
Diagnosing ML
diagnose ML methods by comparing training error with validation error and (if available) some baseline; baseline can be obtained via the Bayes risk when using a probabilistic model (such as the i.i.d. assumption) or human performance or the performance of existing ML methods ("experts" in regret framework)
In what follows, we tacitly assume that data points can (to a good approximation) be interpreted as realizations of iid RVs (see Section Probabilistic Models for Data ). This “i.i.d. assumption” underlies ERM as the guiding principle for learning a hypothesis with small risk. This assumption also motivates to use the average loss \eqref{equ_def_training_val_val} on a validation set as an estimate for the risk. More fundamentally, we need the i.i.d. assumption to define the concept of risk as a measure for how well a hypothesis predicts the labels of arbitrary data points.
Consider a ML method which uses Algorithm alg:validated_ERM (or Algorithm alg:kfoldCV_ERM) to learn and validate the hypothesis [math]\hat{h} \in \hypospace[/math]. Besides the learnt hypothesis
[math]\hat{h}[/math], these algorithms also deliver the training error [math]\trainerror[/math] and the validation error [math]\valerror[/math]. As we will see shortly, we can diagnose ML methods to some extent just by comparing training with validation errors. This diagnosis is further enabled if we know a baseline [math]\benchmarkerror[/math] .
One important source of a baseline [math]\benchmarkerror[/math] are probabilistic models for the data points (see Section A Probabilistic Analysis of Generalization ). Given a probabilistic model, which specifies the probability distribution [math]p(\featurevec,\truelabel)[/math] of the features and label of data points, we can compute the minimum achievable risk. Indeed, the minimum achievable risk is precisely the expected loss of the Bayes estimator [math]\hat{h}(\featurevec)[/math] of the label [math]\truelabel[/math], given the features [math]\featurevec[/math] of a data point. The Bayes estimator
[math]\hat{h}(\featurevec)[/math] is fully determined by the probability distribution [math]p(\featurevec,\truelabel)[/math] of the features and label of a (random) data point [14](Chapter 4).
A further potential source for a baseline [math]\benchmarkerror[/math] is an existing, but for some reason unsuitable, ML method. This existing ML method might be computationally too expensive to be used for the ML application at end. However, we might still use its statistical properties as a benchmark. The We might also use the performance of human experts as a baseline. If we want to develop a ML method that detects certain type of skin cancers from images of the skin, a benchmark might be the current classification accuracy achieved by experienced dermatologists [15].
We can diagnose a ML method by comparing the training error [math]\trainerror[/math] with the validation error [math]\valerror[/math] and (if available) the benchmark [math]\benchmarkerror[/math].
- [math]\trainerror \approx \valerror \approx \benchmarkerror[/math]: The training error is on the same level as the validation error and the benchmark error. There is not much to improve here since the validation error is already on the desired error level. Moreover, the training error is not much smaller than the validation error which indicates that there is no overfitting. It seems we have obtained a ML method that achieves the benchmark error level.
- [math]\valerror \gg \trainerror[/math]: The validation error is significantly larger than the training error. It seems that the ERM results in a hypothesis [math]\hat{h}[/math] that overfits the training set. The loss incurred by [math]\hat{h}[/math] on data points outside the training set, such as those in the validation set, is significantly worse. This is an indicator for overfitting which can be addressed either by reducing the effective dimension of the hypothesis space or by increasing the size of the training set. To reduce the effective dimension of the hypothesis space we have different options depending on the used model. We might use a small number of features in a linear model, a smaller maximum depth of decision trees (Section Decision Trees ) or a fewer layers in an ANN (Section Deep Learning ). One very elegant means for reducing the effective dimension of a hypothesis space is by limiting the number of gradient descent (GD) steps used in gradient-based methods. This optimization based shrinking of a hypothesis space is referred to as early stopping. More generally, we can reduce the effective dimension of a hypothesis space via regularization techniques (see Chapter Regularization ).
- [math]\trainerror \approx \valerror\gg \benchmarkerror[/math]: The training error is on the same level as the validation errorand both are significantly larger than the baseline. Since the training error is not much smaller than the validation error, the learnt hypothesis seems to not overfit the training set. However, the training error achieved by the learnt hypothesis is significantly larger than the benchmark error level. There can be several reasons for this to happen. First, it might be that the hypothesis space used by the ML method is too small, i.e., it does not include a hypothesis that provides a good approximation for the relation between features and label of a data point. The remedy for this situation is to use a larger hypothesis space, e.g., by including more features in a linear model, using higher polynomial degrees in polynomial regression, using deeper decision trees or having larger ANNs (deep ANN (deep net)s). Another reason for the training error being too large is that the optimization algorithm used to solve ERM is not working properly. When using gradient-based methods (see Section GD for Linear Regression ) to solve ERM, one reason for [math]\trainerror \gg \benchmarkerror[/math] could be that the learning rate [math]\lrate[/math] in the GD step is chosen too small or too large (see Figure fig_small_large_lrate-(b)). This can be solved by adjusting the learning rate by trying out several different values and using the one resulting in the smallest training error. Another option is derive optimal values for the learning rate based on a probabilistic model for how the data points are generated. One example for such a probabilistic model is the i.i.d. assumption that has been used in Section A Probabilistic Analysis of Generalization to analyze linear regression methods.
- [math]\trainerror \gg \valerror [/math]: The training error is significantly larger than the validation error (see Exercise). The idea of ERM is to approximate the risk of a hypothesis by its average loss on a training set [math]\dataset = \{ (\featurevec^{(\sampleidx)},\truelabel^{(\sampleidx)}) \}_{\sampleidx=1}^{\samplesize}[/math].The mathematical underpinning for this approximation is the law of large numbers which characterizes the average of (realizations of) iid RVs. The quality and usefulness of this approximation depends on the validity of two conditions. First, the data points used for computing the average loss should be such that they would be typically obtained as realizations of iid RVs with a common probability distribution. Second, the number of data points used for computing the average loss must be sufficiently large. Whenever the data points behave different than the the realizations of iid RVs or if the size of the training set or validation set is too small, the interpretation (comparison) of training error and validation errors becomes more difficult. As an extreme case, it might then be that the validation error consists of data points for which every hypothesis incurs small average loss. Here, we might try to increase the size of the validation set by collecting more labeled data points or by using data augmentation (see Section Data Augmentation ). If the size of training set and validation set are large but we still obtain [math]\trainerror \gg \valerror [/math], one should verify if data points in these sets conform to the i.i.d. assumption. There are principled statistical methods that allow to test if an i.i.d. assumption is satisfied (see [9] and references therein).
Notes
General References

Jung, Alexander (2022). Machine Learning: The Basics. Signapore: Springer. doi:10.1007/978-981-16-8193-6.
Jung, Alexander (2022). "Machine Learning: The Basics". arXiv:1805.05052.
References
- R. Muirhead. Aspects of Multivariate Statistical Theory John Wiley \& Sons Inc., 1982
- J. Larsen and C. Goutte. On optimal data split for generalization estimation and model selection. In IEEE Workshop on Neural Networks for Signal Process 1999
- B. Efron and R. Tibshirani. Improvements on cross-validation: The 632+ bootstrap method. Journal of the American Statistical Association 92(438):548--560, 1997
- 4.0 4.1 4.2 T. Hastie, R. Tibshirani, and J. Friedman. The Elements of Statistical Learning Springer Series in Statistics. Springer, New York, NY, USA, 2001
- I. Cohen and B. Berdugo. Noise estimation by minima controlled recursive averaging for robust speech enhancement. IEEE Sig. Proc. Lett. 9(1):12--15, Jan. 2002
- P. Huber. Approximate models. In C. Huber-Carol, N. Balakrishnan, M. Nikulin, and M. Mesbah, editors, Goodness-of-Fit Tests and Model Validity. Statistics for Industry and Technology. Birkhäuser, Boston, MA, 2002
- 7.0 7.1 7.2 D. Bertsekas and J. Tsitsiklis. Introduction to Probability Athena Scientific, 2 edition, 2008
- R. G. Gallager. Stochastic Processes: Theory for Applications Cambridge University Press, 2013
- 9.0 9.1 H. Lütkepohl. New Introduction to Multiple Time Series Analysis Springer, New York, 2005
- K. V. Mardia, J. T. Kent, and J. M. Bibby. Multivariate Analysis Academic Press, 1979
- K. Young. Bayesian diagnostics for checking assumptions of normality. Journal of Statistical Computation and Simulation 47(3--4):167 -- 180, 1993
- O. Vasicek. A test for normality based on sample entropy. Journal of the Royal Statistical Society. Series B (Methodological) 38(1):54--59, 1976
- M. Belkin, D. Hsu, S. Ma, and S. Mandal. Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences 116(32):15849--15854, 2019
- E. L. Lehmann and G. Casella. Theory of Point Estimation Springer, New York, 2nd edition, 1998
- A. Esteva, B. Kuprel, R. A. Novoa, J. Ko, S. M. Swetter, H. M. Blau, and S. Thrun. Dermatologist-level classification of skin cancer with deep neural networks. Nature 542, 2017