The Basics

This article was automatically generated from a tex file and may contain conversion errors. If permitted, you may login and edit this article to improve the conversion.

Supervised Learning

While there are different kinds of machine learning, we will be focusing on supervised learning. Supervised learning is a machine learning paradigm where the available data consists of a pairing of inputs with know, correct, outputs. What is unknown is exactly how the mapping between those inputs and outputs works. The goal is to infer, from the available data, the general structure of the mapping in the hope that this will generalize to unseen situations. Formally we can state the problem as follows.

The supervised learning problem Given an unknown function [math]f:X \to Y[/math] between spaces [math]X[/math] and [math]Y[/math], find a good approximation of [math]f[/math] using only a dataset of [math]N[/math] samples:

[[math]] \begin{equation*} \mathcal{D} = \big\{ \left( x_i, y_i \right) \big\}_{i=1}^N \quad\text{ with }\quad y_i = f(x_i) \quad\text{for all $i=1 \ldots N$}. \end{equation*} [[/math]]

The space [math]X[/math] is also called the feature space and its elements are referred to as feature vectors. The space [math]Y[/math] is also called the label space and its elements are referred to as labels.

Example

Let [math]X[/math] be the space of all images of cats and dogs and [math]f[/math] the classifier that maps to [math]Y=\left\{ \text{”dog”}, \text{”cat”} \right\}[/math]. Which we can express numerically as [math]X = [0,1]^{3 \times H \times W}[/math] (i.e. an image of height [math]H[/math] and width [math]W[/math] with 3 color channels) and [math]Y=[0,1]^2[/math] (one probability for each of the two classes).

The general approach to solving this problem consists of three main steps.

Choose a model [math]F:X \times W \to Y[/math] parametrized by a parameter space [math]W[/math] ([math]W[/math] for weights, since that is how parameters in NNs are often referred to).
We need to quantify the quality of the model's output, so we need to choose a loss function [math]\ell: Y \times Y \to \mathbb{R}[/math], where [math]\ell(y_1,y_2)[/math] indicates “how different” [math]y_1[/math] and [math]y_2[/math] are.
Based on the dataset and the loss function choose [math]w \in W[/math] so that [math]F(\ \cdot\ ; w)[/math] is the “best” possible approximation of the target function [math]f[/math].

This high-level approach leaves some open questions however.

How to choose the model?
How to choose the loss function?
How to optimize?

None of these questions have canonical answers and are largely handled by trial-and-error and heuristics simply because we have to resolve them before we can make any progress. Regardless, these choices will have a large impact on the final result even though they are in no way supported by the available data or some form of first principle. The collective set of assumptions we make to be able to proceed with the problem is called inductive bias in the machine learning field. For the purpose of this course we will of course pick neural networks as our models of choice and we will talk about those later. The second thing we have to do is chose a loss function. A loss function is a function [math]\ell:Y\times Y \to \mathbb{R}[/math], it works much like a metric, but it is less restrictive.

Usually but not always [math]Y \times Y \to \mathbb{R}^+[/math]
Since we want to minimize loss, the minimum should exist so that [math]\min_{y \in Y} \ell(y_0,y)[/math] is well posed.
Differentiable (a.e. at least) would be necessary since we want to do gradient descent.
Metric properties like identity of indiscernibles, symmetry and triangle inequality need not hold.

Having chosen a model and a loss function we move on to optimization, or: what is the “best” choice of [math]w \in W[/math]? The straightforward (but not necessarily preferred) answer: minimize the loss on the dataset, i.e. find:

[[math]] \begin{equation*} w^* = \argmin_{w \in W} \sum_{i=1}^N \ell \left( F(\, x_i\,;w), y_i \right) . \end{equation*} [[/math]]

Example [Linear least squares]

[[math]] \begin{equation*} F(x;w) = \sum_{j=1}^n w_j \varphi_j(x) \end{equation*} [[/math]]

and [math]\ell(y_1,y_2)=| y_1 - y_2 |^2[/math] for some basis functions [math]\{ \varphi_j \}_j[/math]. Then we get the familiar linear least square setting.

What is the “best” [math]w\in W[/math] is not necessarily the one that minimizes the loss on the dataset, overfitting is often an issue in any optimization problem. Which brings us to regularization. We will discuss regularization techniques for NNs more in the future. But for now we will mention that parameter regularization is a common technique from regression that is often used in NNs. This type of regularization is characterized by the addition of a penalty term to the data loss that discourages parameter values for straying into undesirable areas (such as becoming too large). The modified optimization problem becomes:

[[math]] \begin{equation*} w^* = \argmin_{w \in W} \sum_{i=1}^N \ell \left( F(x_i;w), y_i \right) + \lambda C(w) \end{equation*} [[/math]]

with [math]\lambda \gt 0[/math] and [math]C:W \to \mathbb{R}^+[/math] to penalize complexity in some fashion.

Example [Tikhonov regularization]

[math]W=\mathbb{R}^n[/math] and [math]C(w) = \| w \|^2[/math]. In the context of neural networks this type of parameter regularization is also called weight decay.

Regression & classification Supervised learning should sound familiar by now. Indeed if [math]X=\mathbb{R}^n[/math] and [math]Y=\mathbb{R}^m[/math] then it amounts to regression. Regression is a large part of supervised learning but it is more generally formulated so that is encompasses other tasks such as classification. Classification is the ML designation for (multiclass) logistic regression where [math]X=\mathbb{R}^n[/math] and we try to assign each [math]x \in X[/math] to one of [math]m[/math] classes. The numeric output for this type of problem is normally a discrete probability distribution over [math]m[/math] classes:

[[math]] \begin{equation*} Y = \left\{ (y_1,\ldots,y_m) \in [0,1]^m \ \middle| \ \textstyle\sum_{i=1}^m y_i = 1 \right\}. \end{equation*} [[/math]]

Example example is of this type.

[Statistical learning theory viewpoint]

In SLT the assumption is made that the data samples [math](x_i,y_i)[/math] are drawn i.i.d. from some probability distribution [math]\mu[/math] on [math]X \times Y[/math]. Think about why this is a fairly big leap. What we are then interested in is minimizing the population risk:

[[math]] \begin{equation*} R(w) := \mathbb{E}_{(x,y) \sim \mu} \left[ \ell\left( F(x;w), y \right) \right] := \int_{X \times Y} \ell\left( F(x;w), y \right) d\mu(x,y) . \end{equation*} [[/math]]

The goal would be finding the parameter set that minimizes this population risk:

[[math]] \begin{equation*} w^* = \argmin_{w \in W} R(w). \end{equation*} [[/math]]

But in reality we do not know [math]\mu[/math] and so we cannot even calculate the population risk, let alone minimize it. So we do the next best thing: minimize the empirical risk:

[[math]] \begin{equation*} \hat{R}(w) := \frac{1}{N} \sum_{i=1}^N \ell\left( F(x_i;w), y_i \right) . \end{equation*} [[/math]]

The parameter set that minimize the empirical risk is called the empirical minimizer:

[[math]] \begin{equation*} \hat{w} = \argmin_{w \in W} \hat{R}(w), \end{equation*} [[/math]]

which is the same thing as minimizing the loss on the dataset in the supervised learning setting. When we add a regularization term as before it is called structural risk minimization.

[[math]] \begin{equation*} \hat{w} = \argmin_{w \in W} \hat{R}(w) + \lambda C(w). \end{equation*} [[/math]]

SLT is then concerned with studying things such as bounds on [math]\hat{R}(\hat{w})-R(w^*)[/math]. For more see 2MMS80 Statistical Learning Theory.

Artificial Neurons & Activation Functions

As the name suggests, artificial neural networks are inspired by biology. Just like their biological counterparts their constituent parts are artificial neurons. The basic structure of a biological neuron is illustrated in Figure figure. Each neuron can send and receive signals to and from other neurons so that together they form a network.

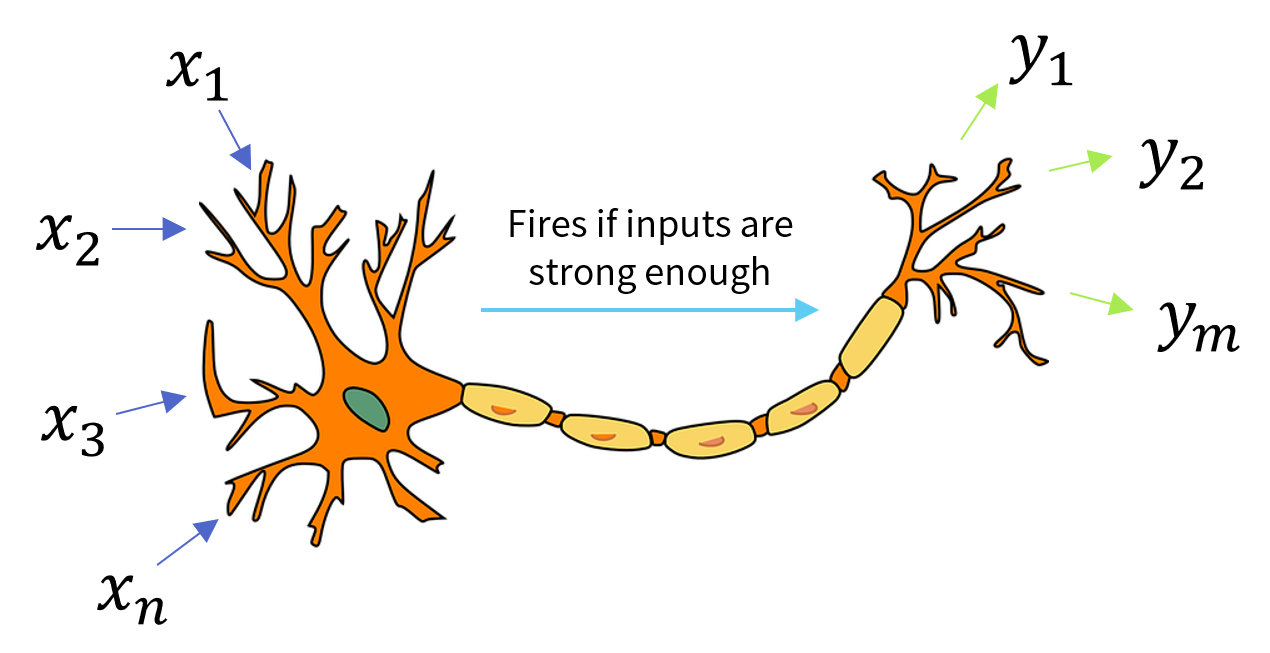
A simplified biological neuron. The dendrites on the left receive electric signals from other neurons, once a certain threshold is reached the neuron will fire a signal along its axon and through its synapses on the right relay a signal to other neurons.

In similar fashion artificial neural networks consist of artificial neurons. Each artificial neurons takes some inputs (usually in the form of real numbers) and produces one or more outputs (again, usually real numbers) that it passes to other neurons. The most common model neuron is given by an affine transform followed by a non-linear function. Let [math]\boldsymbol{x} \in \mathbb{R}^n[/math] be the input signal and [math]\boldsymbol{y} \in \mathbb{R}^m[/math] be the output signal then we calculate

[[math]] \begin{equation} \label{eq:affineneuron} \boldsymbol{y} = \sigma ( A \boldsymbol{x} + \boldsymbol{b}), \end{equation} [[/math]]

where [math]A \in \mathbb{R}^{m \times n}[/math], [math]\boldsymbol{b} \in \mathbb{R}^m[/math] and [math]\sigma[/math] is a choice of activation function. The components of the matrix [math]A[/math] are referred to as the linear weights, the vector [math]\boldsymbol{b}[/math] is called the bias. The intermediate value [math]A \boldsymbol{x} + \boldsymbol{b}[/math] is sometimes referred to as the activation. The activation function [math]\sigma[/math] is also sometimes called the transfer function or the non-linearity. Inputs and outputs need not span the real numbers. Depending on the application we could encounter:

[math]\{0, 1\}[/math]: binary,
[math]\mathbb{R}^+[/math]: non-negative reals,
[math][0,1][/math]: intervals (probabilities for example),
[math]\mathbb{C}[/math]: complex,
etc.

A historically significant choice of activation function is the Heaviside function, given by

[[math]] \begin{equation*} H(x) := \mathbb{1}_{x \geq 0}(x) := \begin{cases} 1 \qquad &\text{if } x \geq 0, \\ 0 &\text{else}. \end{cases} \end{equation*} [[/math]]

A neuron of the type \ref{eq:affineneuron} that uses the Heaviside function as its activation function is called a perceptron. Let us see what we can do with it. Let [math]\boldsymbol{w} \in \mathbb{R}^n[/math] and [math]b \in \mathbb{R}[/math] then a neuron with input [math]\boldsymbol{x} \in \mathbb{R}^n[/math] and output [math]y \in \mathbb{R}[/math] would look like

[[math]] \begin{equation*} \mathcal{N}(\boldsymbol{x}) = H(\boldsymbol{w}^T \boldsymbol{x} + b) = \begin{cases} 1 \qquad &\text{if } \boldsymbol{w}^T \boldsymbol{x} \geq -b, \\ 0 &\text{if } \boldsymbol{w}^T \boldsymbol{x} \lt -b. \end{cases} \end{equation*} [[/math]]

Which is nothing but a linear binary classifier on [math]\mathbb{R}^n[/math] since [math]\boldsymbol{w}^T \boldsymbol{x} = -b[/math] is a hyperplane in [math]\mathbb{R}^n[/math]. This hyperplane divides the space into two and assign the value [math]0[/math] to one half and [math]1[/math] to the other.

Example [Boolean gate]

We can (amongst other things) use a perceptron to model some elementary Boolean logic. Let [math]x_1,x_2 \in \{0,1\}[/math] and let [math]\operatorname{AND}(x_1,x_2) := H(x_1+x_2-1.5)[/math] then the neuron behaves as follows.

[math]x_1[/math]	[math]x_2[/math]	[math]\operatorname{AND}(x_1,x_2)[/math]
0	0	0
0	1	0
1	0	0
1	1	1

The Heaviside function is an example of a scalar or pointwise activation function. Often when a use a scalar function as activation function we abuse notation to let it accepts vector (and matrices) as follows. Let [math]\sigma: \mathbb{R} \to \mathbb{R}[/math] then we allow

[[math]] \begin{equation*} \sigma \left( \begin{bmatrix} x_1 \\ \vdots \\ x_n \end{bmatrix} \right) \equiv \begin{bmatrix} \sigma(x_1) \\ \vdots \\ \sigma(x_n) \end{bmatrix} . \end{equation*} [[/math]]

We list some commonly used scalar activation functions which are also illustrated in Figure figure.

Rectified Linear Unit (ReLU): arguably the most used activation function in modern neural networks, it is calculated as
[[math]] \begin{equation*} \sigma(\lambda) = \relu(\lambda) := \max\{0, \lambda \} . \end{equation*} [[/math]]
Sigmoid (also known as logistic sigmoid or soft-step):
[[math]] \begin{equation*} \sigma(\lambda) := \frac{1}{1 + e^{-\lambda}} . \end{equation*} [[/math]]
The sigmoid was commonly used as activation function in early neural networks, which is the reason that activations functions in general are still often labeled with a [math]\sigma[/math].
Hyperbolic tangent: very similar to the sigmoid, it is given by
[[math]] \begin{equation*} \tanh(\lambda) := \frac{e^\lambda - e^{-\lambda}}{e^{\lambda}+e^{-\lambda}} . \end{equation*} [[/math]]
Swish: a more recent choice of activation function that can be thought of as a smooth variant of the ReLU. It is given by the multiplication of the input itself with the sigmoid function:
[[math]] \begin{equation*} \operatorname{swish_\beta}(\lambda) := \lambda \, \sigma(\beta\lambda) := \frac{\lambda}{1 + e^{-\beta \lambda}} , \end{equation*} [[/math]]
where [math]\beta \gt 0[/math]. The [math]\beta[/math] parameter is usually chosen to be [math]1[/math] but could be treated as a trainable parameter if desired. In case of [math]\beta=1[/math], this function is also called the sigmoid-weighted linear unit or SiLU.

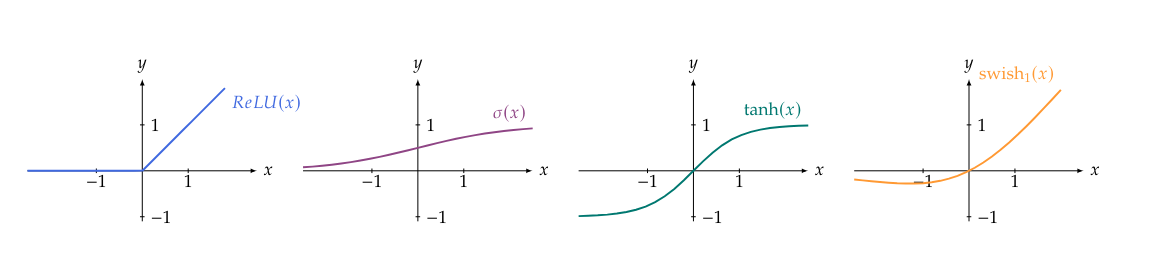
Some common scalar activation functions. From left to right: the rectified linear unit, the logistic sigmoid, the hyperbolic tangent and the swish function with [math]\beta=1[/math].

Activation functions need not be scalar, we list some common multivariate functions.

Softmax, also known as the normalized exponential function: [math]\operatorname{softmax}:\mathbb{R}^n \to [0,1]^n[/math] is given by
[[math]] \begin{equation*} \operatorname{softmax} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \frac{1}{\sum_{i=1}^n e^{x_i}} \begin{bmatrix} e^{x_1} \\ e^{x_2} \\ \vdots \\ e^{x_n} \end{bmatrix} . \end{equation*} [[/math]]
Softmax has the useful property that its output is a discrete probability distribution, i.e. each value is a non-negative real in the range [math][0,1][/math], and all the values in its output add up to exactly [math]1[/math].
Maxpool: here each output is the maximum of a certain subset of the inputs: the function [math]\operatorname{maxpool}:\mathbb{R}^n \to \mathbb{R}^m[/math] is given by
[[math]] \begin{equation*} \operatorname{maxpool} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \begin{bmatrix} \max_{j \in I_1} x_j \\ \max_{j \in I_2} x_j \\ \vdots \\ \max_{j \in I_m} x_j \end{bmatrix} . \end{equation*} [[/math]]
Where for each [math]i \in \{ 1, \ldots, m \}[/math] we have a [math]I_i \subset \{1,\ldots,n \}[/math] that specifies over which inputs to take the maximum for each output. Maxpooling can easily be generalised by replacing the max operation with min, the average, the mean, etc.
Normalization, sometimes it is desirable to re-center and re-scale a signal:
[[math]] \begin{equation*} \operatorname{normalize} \left( \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \right) := \begin{bmatrix} \frac{x_1 - \mu}{\sigma} \\[5pt] \frac{x_2 - \mu}{\sigma} \\ \vdots \\ \frac{x_n - \mu}{\sigma} \end{bmatrix} , \end{equation*} [[/math]]
where [math]\mu = \mathbb{E}[\boldsymbol{x}][/math] and [math]\sigma^2 = \Var(\boldsymbol{x})[/math]. There are many variants on normalization where the difference is how [math]\mu[/math] and [math]\sigma[/math] are computed: over time, over subsets of the incoming signals, etc.

All the previous examples of activation functions are deterministic, but stochastic activation functions are also used.

Dropout is a stochastic function that is often used during the training process but is removed once the training is finished. It works by randomly setting individual values of a signal to zero with probability [math]p[/math]:
[[math]] \begin{equation*} \left(\operatorname{dropout}_p(\boldsymbol{x})\right)_i := \begin{cases} 0 \qquad &\text{with probability } p, \\ x_i &\text{with probability } 1-p . \end{cases} \end{equation*} [[/math]]
Heatbath is a scalar function that outputs [math]1[/math] or [math]-1[/math] with a probability that depends on the input:
[[math]] \begin{equation*} \operatorname{heatbath}(\lambda) := \begin{cases} \hphantom{-}1 \qquad &\text{with probability } \frac{1}{1+e^{-\lambda}} \\ -1 \qquad &\text{otherwise}. \end{cases} \end{equation*} [[/math]]

All the activation functions we seen are essentially fixed functions, swish and dropout have a parameter but it is usually fixed to some chosen value. That means that the trainable parameters of a neural network are usually the linear weights and biases. There is however no a-priori reason why that needs to be the case, in fact we will see a class of non-linear operators with trainable parameters at the end of ch:equivariance. Regardless, having parameters in the non-linear part of a network is somewhat rare in practice at the time of this writing.

Shallow Networks

While we are interested in deep networks we start out with a look at shallow networks. Because of their simplicity we can still approach them constructively and gain some intuition about neural networks in general along the way. You can also think about the study of shallow networks as the study of single layers of deep networks. Let us consider a shallow ReLU network with scalar in- and output. Let [math]\boldsymbol{w}=(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}) \in W=(\mathbb{R}^N)^3[/math] be our set of parameters for some [math]N \in \mathbb{N}[/math], then we define our model [math]F:\mathbb{R} \times W \to \mathbb{R}[/math] as

[[math]] \begin{equation} \label{eq:scalarshallownetwork} F(x; \boldsymbol{w}) := \sum_{i=1}^N c_i \, \sigma(a_i x + b_i) , \end{equation} [[/math]]

where [math]\sigma[/math] is the ReLU. Diagrammatically this network is represented in Figure figure.

Diagrammatic representation of a shallow [math]\mathbb{R} \to \mathbb{R}[/math] neural network per \ref{eq:scalarshallownetwork}. In deep learning literature the input and output of a network are often referred to as the input unit respectively the output unit. The intermediate values are often called the hidden units. What is commonly referred to as the *width* and *depth* of the network is also indicated.

We will restrict ourselves to [math]x \in [0,1][/math] for the time being. In practice this would not be much of a restriction since real world data is compactly supported. Let us explore what types of functions our network can express: the output is a linear combination of functions of the type

[[math]] \begin{equation*} x \mapsto \sigma(a x + b) . \end{equation*} [[/math]]

Which, depending on the value of [math]a[/math], gives us one of the following types of functions.

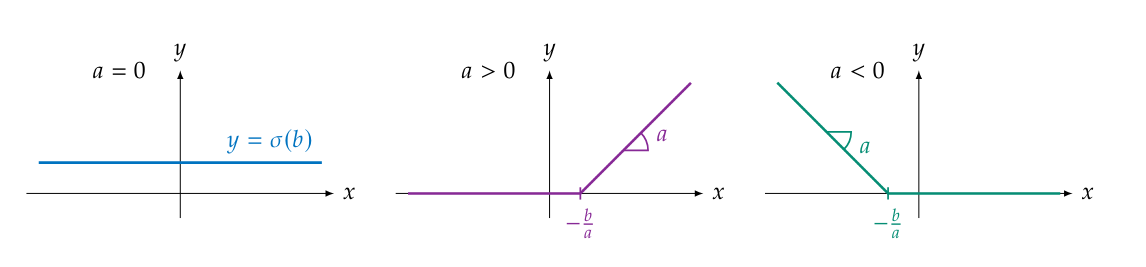
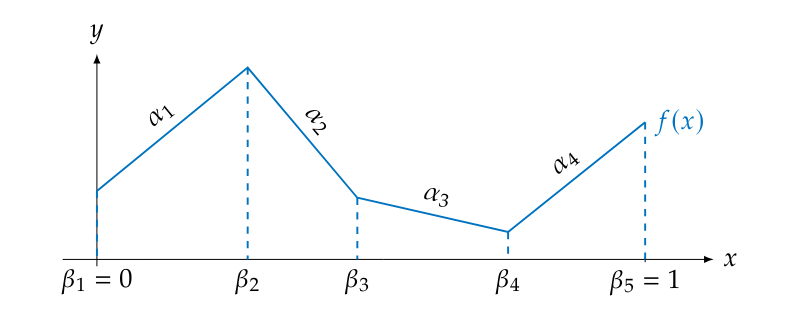
All three of these classes of functions are piecewise linear functions (or piecewise affine functions really), so any linear combination of these functions would again be a piecewise linear function. Hence, our model \ref{eq:scalarshallownetwork} is really just a particular parameterization for a piecewise linear function on [math][0,1][/math]. Can we then represent any piecewise linear function on [math][0,1][/math] by a shallow ReLU network? Let [math]f:[0,1] \to \mathbb{R}[/math] be piecewise linear function with [math]N[/math] pieces. We will denote the inflection points with

[[math]] \begin{equation*} 0 = \beta_1 \lt \beta_2 \lt \ldots \lt \beta_{N+1} = 1 \end{equation*} [[/math]]

and the slopes (i.e. the constant derivatives of each piece) with [math]\alpha_1, \ldots, \alpha_N[/math]. An example of this setup is illustrated in Figure figure.

Example of a piecewise linear function on [math][0,1][/math] with [math]4[/math] pieces. The location of the inflection points are labeled with [math]\beta[/math]'s and the slope of each piece is denoted with an [math]\alpha[/math].

Now choose a network of the type in \ref{eq:scalarshallownetwork} with [math]N+1[/math] neurons:

[[math]] \begin{equation*} F(x) := \sum_{i=1}^{N+1} c_i \, \sigma(a_i x + b_i) . \end{equation*} [[/math]]

Next we choose the parameters [math]\boldsymbol{a},\boldsymbol{b}[/math] and [math]\boldsymbol{c}[/math] of the network as:

[[math]] \begin{align*} & a_{N+1} = 0, & &b_{N+1} = 1, & &c_1=\alpha_1, \\ & a_1, \ldots, a_N = 1, & &b_i = - \beta_i \ (\text{for } i = 1\ldots N), & &c_i=\alpha_i-\alpha_{i-1} \ (\text{for } i=2\ldots N). \end{align*} [[/math]]

This turns our model into

[[math]] \begin{equation} \label{eq:fittedscalarshallow} F(x) = f(0) + \alpha_1 x + \sum_{i=2}^N (\alpha_i - \alpha_{i-1}) \,\sigma(x-\beta_i). \end{equation} [[/math]]

When we examine the third term of \ref{eq:fittedscalarshallow} we see that the ReLU's will vanish each term until [math]x[/math] reaches the appropriate threshold, i.e. [math]\sigma(x-\beta_i) = 0[/math] until [math]x \gt \beta_i[/math]. Hence for [math]x \in [\beta_1,\beta_2][/math] we get the function [math]x \mapsto f(0)+\alpha_1 x[/math] which exactly matches the function [math]f[/math] in that interval. As we proceed to the [math][\beta_2,\beta_3][/math] interval the first term of the right hand sum becomes non-zero and the model becomes

[[math]] \begin{align*} x \mapsto &f(0) + \alpha_1 x + (\alpha_2-\alpha_1)(x-\beta_2) \\ &= f(0) + \alpha_1 x - \alpha_1 x + \alpha_1 \beta_2 + \alpha_2(x-\beta_2) \\ &= f(\beta_2) + \alpha_2 (x-\beta_2), \end{align*} [[/math]]

which is exactly [math]f[/math] in the interval [math][\beta_2,\beta_3][/math]. We can keep advancing along the [math]x[/math]-axis like this and every time we pass an inflection point a new term will activate and bend the line towards a new heading. The model can effectively be rewritten as

[[math]] \begin{equation*} F(x) = \begin{cases} f(0) + \alpha_1 x \quad &\text{if } x \in [\beta_1,\beta_2], \\ f(\beta_2) + \alpha_2 (x-\beta_2) &\text{if } x \in [\beta_2,\beta_3], \\ \qquad \vdots \\ f(\beta_{N-1}) + \alpha_N (x-\beta_{N-1}) &\text{if } x \in [\beta_{N-1},\beta_N], \end{cases} \end{equation*} [[/math]]

which matches [math]f[/math] exactly. Hence, we may conclude that on compact intervals the shallow scalar ReLU neural networks are exactly the space of piecewise linear functions. Piecewise linear function are a simple class of function but can be used to approximate many other classes of function to an arbitrary degree, as the following lemma shows.

Lemma

Let [math]f \in C([0,1],\mathbb{R})[/math] then for all [math]\varepsilon \gt 0[/math] there exists a piecewise linear function [math]F[/math] so that

[[math]] \begin{equation*} \sup_{x\in[0,1]} \left| f(x) - F(x) \right| \lt \varepsilon . \end{equation*} [[/math]]

Show Proof

Let [math]\varepsilon \gt 0[/math] be arbitrary. Since [math]f[/math] is a continuous function on a compact domain it is also uniformly continuous on said domain, i.e.

[[math]] \begin{equation*} \exists \delta \gt 0 \ \forall x_1,x_2 \in [0,1]: |x_1-x_2| \lt \delta \Rightarrow |f(x_1)-f(x_2)| \lt \frac{\varepsilon}{2}. \end{equation*} [[/math]]

Now choose [math]N \gt \frac{1}{\delta}[/math] and partition [math][0,1][/math] as [math]x_i = \frac{i}{N}[/math] for [math]i=0 \ldots N[/math]. Define the piecewise linear function [math]F[/math] as

[[math]] \begin{equation*} F(x) = \sum_{i=1}^N \mathbb{1}_{[x_{i-1},x_i)}(x) \left( f(x_{i-1}) + \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} (x - x_{i-1}) \right) . \end{equation*} [[/math]]

Note that for all [math]i-0 \ldots N[/math] that [math]F(x_i)=f(x_i)[/math]. Now let [math]x \in [0,1][/math] be arbitrary, [math]x[/math] will always fall inside some interval [math][x_{i-1},x_i)[/math] where we have

[[math]] \begin{align*} |f(x)-F(x)| &\leq |f(x)-f(x_i)| + |f(x_i)-F(x)| \\ & \lt \frac{\varepsilon}{2} + |F(x_i)-F(x)| \\ & \lt \frac{\varepsilon}{2} + |F(x_i)-F(x_{i-1})| \\ &= \frac{\varepsilon}{2} + |f(x_i)-f(x_{i-1})| \\ & \lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \end{align*} [[/math]]

■

Since shallow scalar ReLU networks represent the piecewise linear function on [math][0,1][/math] and those piecewise linear functions are dense in [math]C([0,1])[/math] we get the following.

Corollary

Shallow scalar ReLU neural networks of arbitrary width \ref{eq:scalarshallownetwork} are universal approximators of [math]C([0,1])[/math] in the supremum norm.

This corollary is our first universality result. In the context of deep learning, universality is the study of what classes of functions can be approximated arbitrarily well by particular neural networks architectures. Notice that cor:universal has 4 ingredients:

the type of neural network (shallow scalar ReLU network),
the growth direction of the network (width),
the space of function to approximate ([math]C([0,1])[/math]),
and how the approximation is measured (with the supremum norm).

Generalizing this universal approximation result to [math]\mathbb{R}^n[/math] is not possible with just one layer, one of the reasons deep networks are necessary. In general constructive proofs such as for Lemma lemma are not possible/available and we will have to contend ourselves with existence results. Universality is theoretically interesting since it tells us that neural networks can in principle closely approximate most reasonable types of functions (continuous, [math]L^p[/math], etc.), thus explaining to some degree why they are powerful. But universality does not consider many other important facets of neural networks in practice:

economy of representation: how does the number of parameters scale with the desired accuracy,
economy of finding a good approximation: just because a good approximation exist does not mean it is easy to find.

We will not discuss universality further for now. Just remember that, under some mild assumptions, neural networks are universal approximators.

Stochastic Gradient Descent

Recall the elements of supervised learning:

a dataset [math]\mathcal{D} = \{ (x_i,y_i) \in X \times Y \}_{i=1}^N[/math] for some input space [math]X[/math] and output space [math]Y[/math],
a model [math]F:X \times W \to Y[/math] for some parameter space [math]W[/math],
and a loss function [math]\ell:Y \times Y \to \mathbb{R}[/math].

We can then look at the total loss over the dataset for a given choice of parameters:

[[math]] \begin{equation} \label{eq:totaldatasetloss} \ell_{\text{total}}(w) := \frac{1}{|\mathcal{D}|} \sum_{(x,y) \in \mathcal{D}} \ell \left( F(x;w), y \right) . \end{equation} [[/math]]

Note how the loss is a function of the parameters [math]w[/math] only, it could also include some additional regularization terms (as in Section Supervised Learning) but we will leave those details aside for now. Knowing little about [math]F[/math] we cannot find a minimum directly, but assuming everything is differentiable we can use gradient descent:

[[math]] \begin{equation*} w_{t} = w_{t-1} - \eta\, \nabla_{w} \ell_{\text{total}} (w_{t-1}) , \end{equation*} [[/math]]

where [math]\eta \gt 0[/math] is called the learning rate and where we chose some [math]w_0 \in W[/math] as our starting point. Sadly, doing this calculation is not practical in the real world due to:

the datasets being huge,
the models having an enormous amount of parameters.

Just calculating [math]\ell_{\text{total}}[/math] is a major undertaking, calculating [math]\nabla_w \ell_{\text{total}}[/math] is entirely out of the question. Instead, we take a divide and conquer approach. We randomly divide the dataset into (roughly) equal batches and tackle the problem batch by batch. Denote a batch by an index set [math]I \subset \{ 1 \ldots N \}[/math], then we consider the loss over that single batch:

[[math]] \begin{equation} \label{eq:batchloss} \ell_{I}(w) := \frac{1}{|I|} \sum_{i \in I} \ell \left( F(x_i; w), y_i \right) . \end{equation} [[/math]]

Say we divide the dataset into batches [math]I_1,I_2,\ldots, I_B[/math], we can then split our gradient descent step into [math]B[/math] smaller steps:

[[math]] \begin{equation} \label{eq:gradientdescentupdate} w_{t} = w_{t-1} - \eta\, \nabla_w \ell_{I_t}(w_{t-1}) \end{equation} [[/math]]

where we again assume some starting point [math]w_0 \in W[/math]. When we reach [math]t=B[/math] and have exhausted all the batches we say we have complete an epoch. Subsequently, we generate a new set of random batches and repeat the process. This process is called stochastic gradient descent, or SGD for short, the stochastic referring the the random selecting of batches. If the batch [math]I[/math] is uniformly drawn then

[[math]] \begin{equation*} \mathbb{E} \left[ \nabla_w \ell_I(w) \right] = \nabla_w \ell_{\text{total}}(w), \end{equation*} [[/math]]

i.e. the gradient of a uniformly drawn random batch is an unbiased estimator of the gradient of the full dataset.

[Higher order methods]

Gradient descent (stochastic or not) is a first order method since it relies only on the first order derivatives. Higher order methods are rarely used with neural networks because of the large amount of parameters. A model with [math]N[/math] parameters has [math]N[/math] first order derivatives but [math]N^2[/math] second order derivatives, since neural network commonly have millions to billions of parameters calculating second order derivatives is simply not feasible.

A simple but important modification to the (stochastic) gradient descent algorithm is momentum. Instead of taking each step based only on the current gradient we take into account the direction we were moving in in previous steps. The modified gradient descent step is given by

[[math]] \begin{equation*} \begin{split} v_t &= \mu \, v_{t-1} - \eta\,\nabla_w \ell_{I_t}(w_{t-1}), \\ w_t &= w_{t-1} + v_t, \end{split} \end{equation*} [[/math]]

where we initialize with [math]v_0 = 0[/math] and [math]\mu\in[0,1)[/math] is called the momentum coefficient. The variable [math]v_t[/math] can be interpreted as the current velocity vector along which we are moving in the parameter space. At each iteration our new velocity takes a fraction of the previous velocity (controlled by [math]\mu[/math]) and updates it with the current gradient. Observe that for [math]\mu=0[/math], i.e. no momentum, we revert to \ref{eq:gradientdescentupdate}. The larger we take [math]\mu[/math] the more influence the history of the gradients has on our current step.

Training

In practice the training process involves more than applying SGD on the whole dataset. One thing we need to keep in mind is that the dataset is the only real information we have about the underlying function we are trying to approximate, so there is no way to judge how good our approximation is outside of using the dataset. Given that we know that neural networks are universal approximators we can always find a neural networks that perfectly fits any given dataset; making overfitting a given. What we are really after is generalization: the ability of our neural network to give the correct output for inputs it has not seen before. We accomplish this by splitting the dataset and only using part of it to train the network, the remaining part of the dataset (that the network has never seen) we use to test how well our network has generalized. The exact split depends on the situation but using [math]80\%[/math] of the dataset for training and [math]20\%[/math] for testing is a good rule-of-thumb. Let us denote our training and testing datasets as

[[math]] \begin{equation*} \mathcal{D}_{\text{train}} , \mathcal{D}_{\text{test}} \subset \mathcal{D} . \end{equation*} [[/math]]

We then perform SGD on the training dataset, i.e. try to minimize the training loss:

[[math]] \begin{equation} \label{eq:trainingloss} \ell_{\text{train}}(w) := \frac{1}{|\mathcal{D}_{\text{train}}|} \sum_{(x,y) \in \mathcal{D_{\text{train}}}} \ell(F(x;w),y) . \end{equation} [[/math]]

But we judge the performance of our network by the testing loss:

[[math]] \begin{equation} \label{eq:testingloss} \ell_{\text{test}}(w) := \frac{1}{|\mathcal{D}_{\text{test}}|} \sum_{(x,y) \in \mathcal{D_{\text{test}}}} \ell(F(x;w),y) . \end{equation} [[/math]]

By monitoring the testing loss during training we are able to judge for how long we should train, how well our network generalizes and when overfitting sets in. Figure~figure illustrates the typical behaviour of loss curves that are encountered during training.

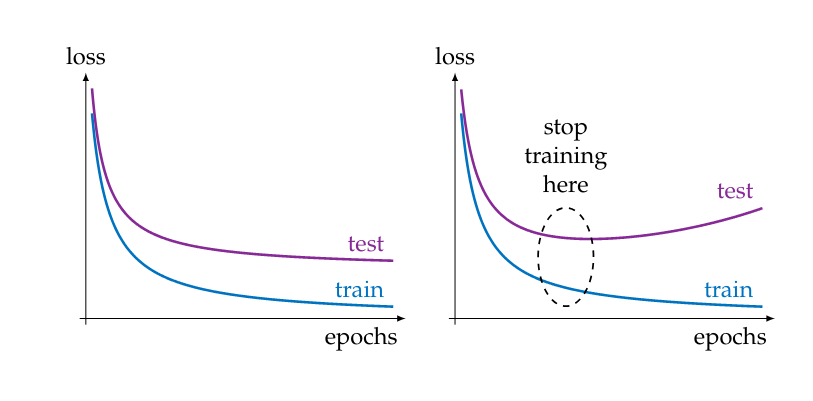
Typical progression of the training and testing loss. The training loss will generally converge to some very low value. The testing loss either behaves in a similar fashion and will converge on some higher value, as is illustrated on the left. The testing loss could also start to increase again at some point, as on the right, this indicates overfitting and tells you when to stop training.

When we are designing a network for a given application we usually do repeated training while we play with the hyperparameters to try and improve the testing loss. This can lead us to overfit the hyperparameters to the given testing dataset. There are two things we can do to mitigate this:

split the dataset in three parts: training/testing/validation,
redo the split randomly every time we retrain.

In the author's opinion the second method is preferable since it is easier to implement and even if the first method is used it is still necessary to redo the split if we decide to make some changes after having used the validation dataset (since if we use it more than once we are back where we started).

[Hyperparameters]

The hyperparameters are all parameters that we ourselves select and are not trainable parts of the model. Examples are: batch size, learning rate, size of the model, choice of activation function, ratio of the dataset split, etc.

General references

Smets, Bart M. N. (2024). "Mathematics of Neural Networks". arXiv:2403.04807 [cs.LG].