Tropical Operators

[math] \newcommand{\ul}{\mathbf} \newcommand{\symbf}{\bm} \newcommand\subsetap{\mathrel{\overset{\makebox[0pt]{\mbox{\normalfont\tiny\sffamily ap.}}}{\rule{0pt}{.8ex}\smash{\subset}}}} \newcommand{\rident}[1]{\mathrm{#1}} \newcommand{\iident}[1]{\mathit{#1}} \newcommand{\wip}{\emoji{construction}} \newcommand{\pointright}{\emoji{backhand-index-pointing-right-light-skin-tone}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\Arg}{Arg} \DeclareMathOperator*{\Var}{Var} \DeclareMathOperator*{\dom}{dom} \DeclareMathOperator{\Div}{div} \DeclareMathOperator{\morph}{\scalebox{0.7}{\ensuremath\square}} \DeclareMathOperator*{\esssup}{ess\,sup} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Cl}{Cl} \DeclareMathOperator{\id}{id} \DeclareMathOperator{\diam}{diam} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\arctantwo}{arctan2} \DeclareMathOperator{\relu}{ReLU} \newcommand{\mathds}{\mathbb}[/math]

This article was automatically generated from a tex file and may contain conversion errors. If permitted, you may login and edit this article to improve the conversion.

We previously generalized the idea of a convolution to that of equivariant linear operators in a Lie group setting, essentially generalizing the domain of our functions. But we can go further by looking at the codomain and generalizing what we mean by `linear'. Linear and non-linear are generally thought of as an absolute dichotomy. Another way of thinking about a linear function or operator is as a map that preserves the algebraic properties of the field of real numbers. But could we not look at maps that preserve the structure of other algebraic structures rather than the field of real numbers? We could in principle develop this idea using any algebraic structure, but to be useful in the context of neural networks we want the underlying set to be numeric and the operations to be able to be performed by a computer. Additionally, restricting ourselves to fields would be very limiting, a more congenial algebraic structure is the semiring. Semirings turn up in many places, indeed the first mathematical structure we learn about, the set of natural numbers [math]\mathbb{N}[/math], is a semiring. Semirings arise in many areas of mathematics such as functional analysis, topology, graphs, combinatorics, optimization, etc. See for an extensive survey of the applications of semirings.

Semirings

A semiring is an algebraic structure in which we can add and multiply elements, but in which neither subtraction nor division are necessarily possible.

Definition (Semiring)

A semiring is a set [math]R[/math] equipped with two binary operations [math]\oplus[/math] and [math]\odot[/math], called addition and multiplication, such that

• addition and multiplication are associative,
• addition is commutative,
• addition has an identity element [math]\mathbb{0}[/math],
• multiplication has an identity element [math]\mathbb{1}[/math],
• multiplication distributes over addition:
  [[math]] \begin{equation*} \begin{split} a \odot (b \oplus c) = a \odot b \oplus a \odot c, \\ (a \oplus b) \odot c = a \odot c \oplus b \odot c, \end{split} \end{equation*} [[/math]]
• multiplication by [math]\mathbb{0}[/math] annihilates:
  [[math]] \begin{equation*} \mathbb{0} \odot a = a \odot \mathbb{0} = \mathbb{0}. \end{equation*} [[/math]]

Additionally if [math]a \oplus a = a[/math] we say the semiring is idempotent and if [math]a \odot b = b \odot a[/math] we say the semiring is commutative or abelian.

Just like with standard multiplication it is conventional to abbreviate [math]a b \equiv a \odot b[/math] if there can be no confusion. We also let [math]\odot[/math] take precedence over [math]\oplus[/math], i.e. [math]a \odot b \oplus c = (a \odot b) \oplus c[/math].

[Rig]

Some works refer to semirings as rigs, from rings `without negatives', hence the missing `n'.

Example [Real linear semiring]

The real numbers form a commutative semiring [math](\mathbb{R},+, \,\cdot\,)[/math] under standard addition and multiplication. Naturally all fields and rings are also semirings.

Example [Viterbi semiring]

The Viterbi semiring is given by the unit interval [math][0,1][/math] and the operations

[[math]] \begin{equation*} \begin{split} a \oplus b &:= \max\{a,b\}, \\ a \odot b &:= a b . \end{split} \end{equation*} [[/math]]

The additive unit is [math]0[/math] and multiplicative unit is [math]1[/math]. This semiring is both idempotent and commutative. Note that there exists no element [math](-a)[/math] so that [math]a \oplus (-a) = \mathbb{0}=0[/math] and no element [math]a^{-1}[/math] so that [math]a \odot a^{-1} = \mathbb{1}=1[/math]. So neither subtraction nor division is possible in this semiring.

Example [Log semiring]

The log semiring is given by the set [math]\mathbb{R} \cup \{ -\infty,\,+\infty\}[/math] and the operations

[[math]] \begin{equation*} \begin{split} a \oplus b &:= \log \left( e^a + e^b \right), \\ a \odot b &:= a + b. \end{split} \end{equation*} [[/math]]

The additive unit is [math]-\infty[/math] and the multiplicative unit is [math]0[/math].

The central object of study in linear algebra is the vector space over a field (usually [math]\mathbb{R}[/math] or [math]\mathbb{C}[/math]). The analogue to the vector space in our generalized setting is the semimodule.

Definition (Semimodule)

Let [math](R,\oplus,\odot)[/math] be a semiring. A left [math]R[/math]-semimodule or semimodule over [math]R[/math] is a commutative monoid [math](M,+)[/math] with additive identity [math]0_M[/math] and a map [math]R \times M \to M[/math] denoted by [math](a,m) \mapsto a m[/math], called scalar multiplication, so that for all [math]a,b \in R[/math] and [math]m,m' \in M[/math] the following hold:

• [math](a \odot b) m = a (b m)[/math],
• [math]a(m+m')=a m + a m'[/math],
• [math](a \oplus b)m=a m + b m[/math],
• [math]\mathbb{1} m = m[/math],
• [math]a 0_M = 0_M = \mathbb{0} m[/math].

Naturally every semiring is a semimodule over itself just like every field is a vector space over itself.

Example

Let [math]R[/math] be a semiring and [math]S[/math] a non-empty set, then [math]R^S[/math] (the set of all functions [math]S \to R[/math]) is a semimodule with addition and scalar multiplication defined element-wise: let [math]f,f' \in R^S[/math] and [math]r \in R[/math] then

[[math]] \begin{equation*} (f \oplus f')(s) := f(s) \oplus f'(s) \quad \text{and} \quad (r \odot f)(s) := r \odot f(s) \end{equation*} [[/math]]

for all [math]s \in S[/math]. Here we used [math]\oplus[/math] and [math]\odot[/math] for the operations in the semimodule as well since they correspond with the [math]\oplus[/math] and [math]\odot[/math] operations in the semiring. The additive identity of the semimodule is the constant function [math]s \mapsto \mathbb{0}[/math]. This generalizes the prototypical vector space [math]\mathbb{R}^n[/math] to the semimodule [math]R^n[/math] using the notational convention [math]n\equiv\{1,\ldots,n\}[/math]. For non-finite [math]S[/math] we get the generalization of function vector spaces to function semimodules.

Example

Let [math]R=([0,1],\max,\,\cdot\,)[/math] be the Viterbi semiring from Example example and let [math]S[/math] be a manifold. Let [math]f,f': S \to [0,1][/math] and define addition and scalar multiplication as

[[math]] \begin{equation*} (f + f')(s) := \max \left\{ f(s) ,\, f'(s)\right\} \quad \text{and} \quad (r f)(s) := r f(s), \end{equation*} [[/math]]

then the functions from [math]S[/math] to [math][0,1][/math] form a semimodule.

Now we can formulate a generalization of linear maps in the form of semiring homomorphisms.

Definition (Semimodule homomorphism)

Let [math]R[/math] be a semiring and let [math]X[/math] and [math]Y[/math] be semimodules over [math]R[/math]. Then a map [math]A:X \to Y[/math] is an [math]R[/math]-homomorphic map or an [math]R[/math]-homomorphism if for all [math]a,b \in R[/math] and [math]f,f' \in X[/math]:

[[math]] \begin{equation*} A(a f + b f') = a (A f) + b (A f') , \end{equation*} [[/math]]

where on the left the addition and scalar multiplication happen in [math]X[/math] and on the right the addition and scalar multiplication happen in [math]Y[/math].

Just like with the definition of linearity the single condition above is equivalent to the following two conditions:

[[math]] \begin{equation*} A(a f) = a (A f') \quad \text{and} \quad A(f + f') = A f + A f' \qquad \forall a \in R ,\, f,f' \in X. \end{equation*} [[/math]]

Under this definition we can understand linear as meaning homomorphic with respect to the real linear semigroup [math](\mathbb{R},+,\,\cdot\,)[/math]. But now, instead of just considering linear maps we can pick another semigroup and consider homomorphisms with respect to this semigroup. This allows us to construct equivariant semimodule homomorphic operators in the same fashion as we did with equivariant linear operators in section Equivariant Linear Operators. We will develop such a class of equivariant operators for a particular choice of semiring.

Tropical Semiring

Definition (Tropical semiring)

The max tropical semiring or max-plus algebra or simply tropical semiring is the semiring [math]\mathbb{R}_{\max}:=\left(\mathbb{R} \cup \{-\infty\} ,\oplus,\odot \right)[/math], with the operations

[[math]] \begin{equation*} \begin{split} a \oplus b &:= \max\{a, b\} , \\ a \odot b &:= a + b. \end{split} \end{equation*} [[/math]]

Where the additive identity is [math]\mathbb{0}:=-\infty[/math] and the multiplicative identity is [math]\mathbb{1}:=0[/math].

Since [math]a \oplus a = \max \{ a, a \} = a[/math] and [math]a \odot b = a+b=b+a = b \odot a[/math] the tropical semiring is both idempotent and commutative. By definition we set [math]a + (-\infty) := -\infty[/math] so that we satisfy the annihilation property [math]a \odot \mathbb{0} = \mathbb{0} \odot a = \mathbb{0}[/math].

The tropical semiring can alternatively be defined as [math](\mathbb{R} \cup \{ +\infty \}, \min, +)[/math], which is then also called the min tropical semiring or min-plus algebra. But we observe that one is isomorphic to the other via negation so we make a style choice and go with the max version.

Example [ReLU]

Recall that the rectified linear unit is defined as [math]x \mapsto \{ x,\, 0\}[/math] for [math]x \in \mathbb{R}[/math]. In the tropical setting we can write this as [math]x \mapsto x \oplus 0[/math] for [math]x \in \mathbb{R}_{\max}[/math], hence the ReLU may not be a linear or affine function but it is tropically affine. So we can think about a typical ReLU neural network as really alternating operations from two distinct semirings.

We based our construction of equivariant linear operators on integration. When you consider an integral as a limit of a sum of products we can see how we could define a type of integration with respect to another semigroup. Recall that Riemannian integration is defined in terms of Darboux sums over ever smaller partitions of the underlying space. Let [math]M[/math] be a manifold with some Radon measure [math]\mu[/math] and [math](R,\oplus,\odot)[/math] a semiring. Let [math]P[/math] be a partition of [math]M[/math] and define [math]\mu(P) := \sup_{S \in P} \mu(S)[/math]. Then we can generalize a Darboux sum

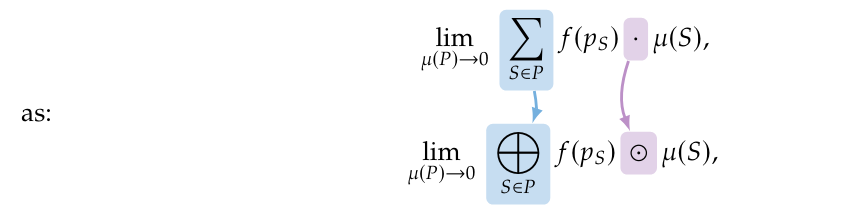
where [math]p_S \in M[/math] is any arbitrary point in the partition element [math]S[/math] and assuming that for all [math]\varepsilon \gt 0[/math] we can find a partition [math]P[/math] so that [math]\mu(P) \lt \varepsilon[/math]. Filling in the tropical semiring operations we obtain:

[[math]] \begin{equation} \label{eq:lim_max_f} \lim_{\mu(P) \to 0}\ \max_{S \in P} \left( f(p_S) + \mu(S) \right) \end{equation} [[/math]]

([math]\mu(S) \to 0[/math] since [math]\mu(P) \to 0[/math])

[[math]] =\lim_{\mu(P) \to 0}\ \max_{S \in P} f(p_S) [[/math]]

(Assuming [math]f[/math] is such that the limit exists and is unique)

[[math]] = \sup_{p \in M} f(p). [[/math]]

Lebesgue integration can be generalized similarly. This would yield the same [math]\sup_{p \in M} f(p)[/math] formula but for all measurable functions that are bounded from above rather then all the functions for which the Darboux sum has a unique limit. We will not detail the Lebesgue construction (see for that) but proceed with the [math]\sup_{p \in M} f(p)[/math] formula as our definition of tropical integral.

Classic example of a function that is Lebesgue integrable but not Riemann integrable is the indicator function of the rational numbers [math]\mathbb{1}_{\mathbb{Q}}[/math]. The limit \ref{eq:lim_max_f} does not exist depending on our choice of points [math]p_S[/math] but in the Lebesgue sense we simply get [math]\sup_{x \in \mathbb{R}} \mathbb{1}_{\mathbb{Q}}(x)=1[/math] as expected.

Definition

Let [math]M[/math] be a manifold, then we define the set of measurable [math]\mathbb{R}_{\max}[/math]-valued functions that are bounded from above as

[[math]] \begin{equation*} \iident{BA}(M) := \iident{BA}(M,\mathbb{R}_{\max}) := \left\{\, f \in \mathbb{R}_{\max}^M \ \middle\vert \ \textstyle\sup_{p \in M} f(p) \lt \infty \ \text{and $f$ is measurable} \, \right\} . \end{equation*} [[/math]]

Additionally if [math]f[/math] is not identical to [math]-\infty[/math] everywhere we say [math]f[/math] is proper.

Clearly BA([math]M[/math]) is a tropical semimodule (i.e. a semimodule with respect to the tropical semiring) under pointwise addition and multiplication:

[[math]] \begin{equation*} (f \oplus f')(p) := \max\{f(p),f'(p)\} \quad \text{and} \quad (a \odot f)(p) := a + f(p) , \end{equation*} [[/math]]

for all [math]a \in \mathbb{R}_{\max}[/math], [math]f,f' \in \iident{BA}(M)[/math] and all [math]p \in M[/math]. The functions in BA([math]M[/math]) are exactly those for which the tropical integral exists.

Definition (Tropical integral)

Let [math]M[/math] be a manifold then we call the mapping [math]\iident{BA}(M) \to \mathbb{R}_{\max}[/math] defined by

[[math]] \begin{equation*} f \mapsto \sup_{p \in M} f(p) \end{equation*} [[/math]]

for [math]f \in \iident{BA}(M)[/math] the tropical integral over [math]M[/math].

We can easily check that the tropical integral is a tropical map (i.e. a semimodule homomorphism with respect to the tropical semiring) from [math]\iident{BA}(M)[/math] to [math]\mathbb{R}_{\max}[/math] in the same way that the (linear) integral is a linear map from the integrable functions to [math]\mathbb{R}[/math]. For all [math]a,b \in \mathbb{R}_{\max}[/math] and [math]f,f' \in \iident{BA}(M)[/math] we have:

[[math]] \begin{equation*} \textstyle \sup_{p \in M} (a \odot f \oplus b \odot f')(p) = a \odot \left( \sup_{p \in M} f(p) \right) \oplus b \odot \left( \sup_{p \in M} f'(p) \right) . \end{equation*} [[/math]]

Let [math]M[/math] be a homogeneous space of the Lie group [math]G[/math], let `[math]\cdot[/math]' denote both the action of [math]G[/math] on [math]M[/math] and the corresponding representation on functions on [math]M[/math]. Since this representation does not affect the codomain of the functions it does not change the supremum, hence the tropical integral is always invariant:

[[math]] \begin{equation*} \sup_{p \in M}\, (g \cdot f)(p) = \sup_{p \in M} f(p). \end{equation*} [[/math]]

So now we have developed an alternative notion of linearity and an alternative to the (linear) invariant integral. We will use these elements to construct a new type of equivariant operator in the same manner as we did before with linear operators.

Equivariant Tropical Operators

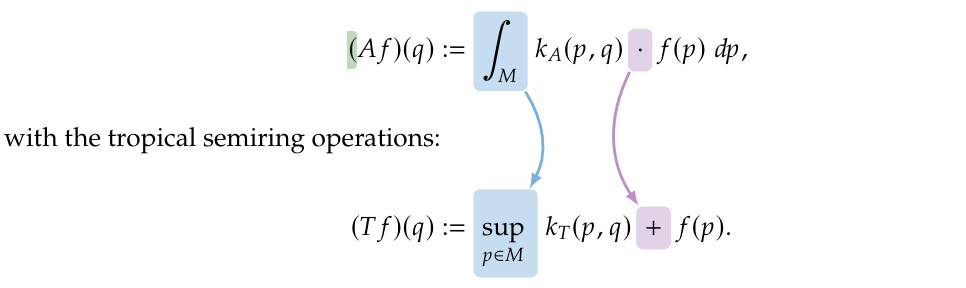
The starting point for our equivariant linear operators was the integral operator from equation. We obtain the tropical analogue simply by replacing the linear semiring operations:

We can see that if [math]k_T \in \iident{BA}(M \times N)[/math] and [math]f \in \iident{BA}(M)[/math] then [math]Tf \in \iident{BA}(N)[/math]. It is straightforward to verify that [math]T[/math] is a tropical operator from [math]\iident{BA}(N)[/math] to [math]\iident{BA}(N)[/math]. Now we can proceed in the exact same way as in section Equivariant Linear Operators to find out when [math]T[/math] is equivariant.

Lemma (Equivariant tropical integral operators)

Let [math]M[/math] and [math]N[/math] be homogeneous spaces of a Lie group [math]G[/math]. Let [math]T[/math] be a tropical integral operator from [math]\iident{BA}(M)[/math] to [math]\iident{BA}(N)[/math] with a kernel [math]k_T \in \iident{BA}(M \times N)[/math]. Then

[[math]] \begin{equation*} T(g\cdot f) = g \cdot (T f) \end{equation*} [[/math]]

for all [math]g \in G[/math] and [math]f \in \iident{BA}(M)[/math] if and only if

[[math]] \begin{equation} \label{eq:tropical_equivariant_kernel_symmetry} k_T(g \cdot p,g \cdot q) = k_T(p,q) \end{equation} [[/math]]

for all [math]g \in G[/math], [math]p \in M[/math] and [math]q \in N[/math].

Show Proof

First we show that [math]T f \in \iident{BA}(N)[/math]:

[[math]] \begin{align*} \sup_{q \in N} \ (T f)(q) &= \sup_{q \in N} \ \left( \sup_{p \in M}\ k_T(p,q) + f(p) \right) \\ &\leq \left(\sup_{(p,q) \in M \times N}\ k_T(p,q)\right) + \left(\sup_{p \in M} f(p)\right) \\ & \lt \infty , \end{align*} [[/math]]

since both [math]k_T[/math] and [math]f[/math] are bounded from above.

“[math]\Rightarrow[/math]” Assuming [math]T[/math] to be equivariant, take an arbitrary [math]g \in G[/math] and [math]f \in \iident{BA}(M)[/math] and substitute the definition of the group representation and [math]T[/math] in

[[math]] \begin{equation*} g^{-1} \cdot T(g\cdot f) = T f \end{equation*} [[/math]]

to find

[[math]] \begin{equation} \label{eq:TLO_1} \sup_{p \in M} k_T(p,g \cdot q) + f (g^{-1} \cdot p) = \sup_{p \in M} k_T(p,q) + f(p) \end{equation} [[/math]]

for all [math]q \in N[/math]. Since the tropical integral is invariant under domain transformation we can substitute [math]p[/math] with [math]g \cdot p[/math] on the left without changing the result:

[[math]] \begin{equation*} \sup_{p \in M} k_T(g \cdot p,g \cdot q) + f (p) = \sup_{p \in M} k_T(p,q) + f(p) \end{equation*} [[/math]]

for all [math]q \in N[/math]. The equality only holds for all [math]f[/math] if

[[math]] \begin{equation} \label{eq:TLO_2} k_T(g \cdot p,g \cdot q) = k_T(p,q) \end{equation} [[/math]]

for all [math]p \in M[/math], [math]q \in N[/math] and [math]g \in G[/math].

“[math]\Leftarrow[/math]”

Assuming [math]k_T(g \cdot p,g \cdot q)=k_T(p,q)[/math] for all [math]g \in G[/math], [math]p \in M[/math] and [math]q \in N[/math] then \ref{eq:TLO_2} follows for any choice of [math]f \in \iident{BA}(M)[/math], [math]g \in G[/math] and [math]q \in N[/math]. Substituting the invariant tropical integral the other way yields \ref{eq:TLO_1}, which implies the equivariance

[[math]] \begin{equation*} g^{-1} \cdot T(g\cdot f) = T f \end{equation*} [[/math]]

since [math]q \in N[/math] is arbitrary. The function [math]f[/math] and group element [math]g[/math] were also chosen arbitrarily so equivariance follows for all [math]f \in \iident{BA}(M)[/math] and [math]g \in G[/math].

■

Now we can use the same strategy as we did in the linear case and use the symmetry \ref{eq:tropical_equivariant_kernel_symmetry} to fix the second argument of the kernel [math]k_T[/math]. Pick a [math]q_0 \in N[/math] then for all [math]q \in N[/math] there exists at least one [math]g_q \in G_{q_0}[/math], consequently

[[math]] \begin{equation*} k_T(p,q) = k_T(p, g_q \cdot q_0) = k_T(g_q \cdot g_q^{-1} \cdot p, g_q \cdot q_0) = k_T(g_q^{-1} \cdot p, q_0) \end{equation*} [[/math]]

for all [math]p \in M[/math] and [math]q \in N[/math]. From which we can define a reduced kernel [math]\kappa_T \in \iident{BA}(M)[/math] as

[[math]] \begin{equation*} \kappa_T(p) := k_A (p, q_0) \end{equation*} [[/math]]

that still allows us to recover the full kernel by

[[math]] \begin{equation*} k_T(p,q) = k_T(g_q^{-1} \cdot p, q_0) = \kappa_T(g_q^{-1} \cdot p) . \end{equation*} [[/math]]

This whole construction in the end gives us the same type of operator as in Theorem theorem but with the linear operations switched for tropical operations:

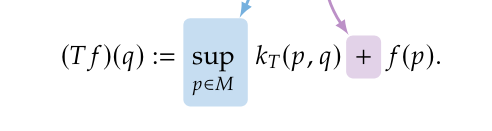
We summarize this result in the following theorem.

Theorem (Equivariant tropical operators)

Let [math]M[/math] and [math]N[/math] be homogeneous spaces of a Lie group [math]G[/math]. Fix a [math]q_0 \in N[/math] and let [math]\kappa_T \in \iident{BA}(M)[/math] be compatible, i.e

[[math]] \begin{equation*} \forall h \in G_{q_0} : h \cdot \kappa_A = \kappa_A. \end{equation*} [[/math]]

Then the operator [math]T[/math] defined by

[[math]] \begin{equation*} (T f)(q) := \sup_{p \in M}\ (g_q \cdot \kappa_T) (p) + f(p) \end{equation*} [[/math]]

where for all [math]q \in N[/math] we choose any [math]g_q[/math] so that [math]g_q \cdot q_0 = q[/math], is a well defined tropical operator from [math]\iident{BA}(M)[/math] to [math]\iident{BA}(N)[/math] that is equivariant with respect to [math]G[/math].

Conversely every tropical integral operator \ref{eq:tropical_integral_operator} with a kernel in [math]\iident{BA}(M \times N)[/math] that is equivariant is of this form.

Show Proof

“[math]\Rightarrow[/math]”

Assume we have a [math]\kappa_T \in \iident{BA}(M)[/math] that is compatible. Define

[[math]] \begin{equation*} k_T(p,q) := (g_q \cdot \kappa_T)(p) \end{equation*} [[/math]]

we can check that [math]k_T[/math] is well defined and satisfies the requirements of Lemma lemma because of the compatibility condition on [math]\kappa_T[/math].

“[math]\Leftarrow[/math]”

Assume we have a tropical integral operator [math]T[/math], then by Lemma lemma we have a kernel [math]k_T \in \iident{BA}(M \times N)[/math] that satisfies \ref{eq:tropical_equivariant_kernel_symmetry}. Fix a [math]q_0 \in N[/math] and define

[[math]] \begin{equation*} \kappa_T(p) := k_T(p,q_0) , \end{equation*} [[/math]]

then we can check that [math]\kappa_T[/math] satisfies the compatibility condition.

■

Example [Max pooling] Let [math]G=(\mathbb{R}^n,+)[/math] be the translation group and [math]M=N=\mathbb{R}^n[/math]. Pick a subset [math]S \subset \mathbb{R}^n[/math] and define

[[math]] \begin{equation*} \kappa_T(p) := \begin{cases} \ 0 & \text{if } p \in S, \\ \ -\infty & \text{elsewhere}. \end{cases} \end{equation*} [[/math]]

Then the corresponding operator [math]T[/math] equals

[[math]] \begin{align*} (T f)(\boldsymbol{y}) &= \sup_{\boldsymbol{x} \in \mathbb{R}^n} (\boldsymbol{y} \cdot \kappa_T)(\boldsymbol{x}) + f(\boldsymbol{x}) \\ &= \sup_{\boldsymbol{x} \in \mathbb{R}^n} \kappa_T(\boldsymbol{x}-\boldsymbol{y}) + f(\boldsymbol{x}) \\ &= \sup_{\boldsymbol{x} \in \boldsymbol{y}+S} f(\boldsymbol{x}) , \end{align*} [[/math]]

so at each point [math]\boldsymbol{y}[/math] the output equals the supremum of the input in the subset [math]\boldsymbol{y}+S[/math]. Think of this a continous version the shift-invariant max pooling operation usually seen in CNNs. In this light we can see that max pooling is a tropical operator.

Example [Tropical convolution] Let [math]G=M=N[/math] be some Lie group, then we call the equivariant tropical operation tropical convolution or morphological convolution, which we denote as

[[math]] \begin{equation*} (\kappa \square_G f)(h) := \sup_{g \in G}\ (h \cdot \kappa)(g) + f(g) . \end{equation*} [[/math]]

The name morphological convolution comes from the field of grayscale morphology where these types of operators have previously been used for image processing applications, see . An example use of these types of operations in neural networks can be found in .

Example [Pointwise ReLU] Let [math]G=M=N[/math] be some Lie group and let [math]f \in \iident{BA}(M)[/math]. Define a kernel

[[math]] \begin{equation*} \kappa_T(g) := \begin{cases} \ 0 \qquad & \text{if } g=e, \\ \ -\sup_{h \in G} f(h) & \text{else.} \end{cases} \end{equation*} [[/math]]

Then applying the corresponding operator to [math]f[/math] gives

[[math]] \begin{align*} (Tf)(h) &= \sup_{g \in G} (h \cdot \kappa_T)(g) + f(g) \\ &= \max \left\{ f(h) ,\, \sup_{g \in G} \left( -\sup_{z \in G} f(z) \right) +f(g) \right\} \\ &= \max \left\{ f(h) ,\, 0 \right\} \\ &= \relu(f(h)) . \end{align*} [[/math]]

We have not said anything about the boundedness of [math]T[/math] in Theorem theorem since it is not clear what metric or norm we should consider on the function space BA. In the following lemma we detail some reasonable conditions under which [math]T[/math] will be bounded in the supremum norm.

Lemma

In the setting of Theorem theorem: if [math]f \in \iident{B}(M)[/math] and [math]\sup_{p \in M} \kappa_T(p)=0[/math] then [math]Tf \in \iident{B}(N)[/math] and [math]T[/math] is a bounded operator from [math]\iident{B}(M)[/math] to [math]\iident{B}(N)[/math] in the supremum norm.

Show Proof

[[math]] \begin{align*} \left\| T f \right\|_\infty &= \sup_{q \in N} \left|\ \sup_{p \in M}\ (g_q \cdot \kappa_T)(p) + f(p) \ \right| \\ &\leq \sup_{q \in N} \left|\ \sup_{p \in M} (g_q \cdot \kappa_T)(p) + \sup_{p \in M} f(p) \ \right| \\ &= \sup_{q \in N} \left|\ \sup_{p \in M} \kappa_T(p) + \sup_{p \in M} f(p) \ \right| \\ &= \left|\ \sup_{p \in M} \kappa_T(p) + \sup_{p \in M} f(p) \ \right| \\ &= \left|\ \sup_{p \in M} f(p) \ \right| \\ &\leq \sup_{p \in M} \left| f(p) \right| \\ &= \left\|\, f \,\right\|_\infty . \end{align*} [[/math]]

■

We have seen how we can use semirings, and the tropical semiring in particular, to develop classes of equivariant operators other than linear. From the examples we saw we can conclude that many operators currently in use in neural networks (particularly the ReLU and max pooling activation functions) are special cases of tropical or tropically affine operators and fit well inside the equivariant semimodule homomorphism framework.

General references

Smets, Bart M. N. (2024). "Mathematics of Neural Networks". arXiv:2403.04807 [cs.LG].