Manifolds

[math] \newcommand{\ul}{\mathbf} \newcommand{\symbf}{\bm} \newcommand\subsetap{\mathrel{\overset{\makebox[0pt]{\mbox{\normalfont\tiny\sffamily ap.}}}{\rule{0pt}{.8ex}\smash{\subset}}}} \newcommand{\rident}[1]{\mathrm{#1}} \newcommand{\iident}[1]{\mathit{#1}} \newcommand{\wip}{\emoji{construction}} \newcommand{\pointright}{\emoji{backhand-index-pointing-right-light-skin-tone}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\Arg}{Arg} \DeclareMathOperator*{\Var}{Var} \DeclareMathOperator*{\dom}{dom} \DeclareMathOperator{\Div}{div} \DeclareMathOperator{\morph}{\scalebox{0.7}{\ensuremath\square}} \DeclareMathOperator*{\esssup}{ess\,sup} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Cl}{Cl} \DeclareMathOperator{\id}{id} \DeclareMathOperator{\diam}{diam} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\arctantwo}{arctan2} \DeclareMathOperator{\relu}{ReLU} \newcommand{\mathds}{\mathbb}[/math]

This article was automatically generated from a tex file and may contain conversion errors. If permitted, you may login and edit this article to improve the conversion.

We start with the basic object we will be working with: the manifold. We are accustomed to doing analysis on [math]\mathbb{R}^n[/math] but we also know that there are non-Euclidean spaces of importance. Classic example is the unit circle [math]S^1[/math], which is distinctly non-Euclidean but still admits derivatives, integrals, PDEs, etc. When working with an object such as [math]S^1[/math] we usually do it indirectly by parameterizing it some way, such as with an angle [math]\theta \in [0,2 \pi)[/math], so that at least locally it resembles [math]\mathbb{R}[/math]. We can generalize this and consider all spaces that we can, at least locally, identify with a subset of [math]\mathbb{R}^n[/math].

Characterization

The proper way to introduce manifolds is starting with a set and then adding several layers of structure, as is done in . After going through that laborious process we would then see a characterization that is a more practical tool for constructing manifolds. In this course we will skip straight to that characterization in the form of the following lemma.

Lemma (Smooth manifold chart lemma)

Let [math]M[/math] be a set and suppose we are given a collection of subsets [math]\{ U_\alpha \}_{\alpha \in I}[/math] of [math]M[/math] for some index set [math]I[/math], together with maps [math]\varphi_\alpha:U_\alpha \to \mathbb{R}^n[/math]. Then [math]M[/math] together with [math]\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}[/math] gives a smooth [math]n[/math]-dimensional manifold if the following conditions are satisfied.

• For all [math]\alpha \in I[/math], [math]\varphi_\alpha[/math] is a bijection between [math]U_\alpha[/math] and an open subset of [math]\mathbb{R}^n[/math].
• For each [math]\alpha,\beta \in I[/math], the sets [math]\varphi_\alpha \left( U_\alpha \cap U_\beta \right)[/math] and [math]\varphi_\beta \left( U_\alpha \cap U_\beta \right)[/math] are open in [math]\mathbb{R}^n[/math].
• When [math]U_\alpha \cap U_\beta \neq \varnothing[/math] then the map [math]\tau_{\alpha,\beta} := \varphi_\beta \circ \varphi_\alpha^{-1} : \varphi_\alpha(U_\alpha \cap U_\beta) \to \varphi_\beta(U_\alpha \cap U_\beta)[/math] is smooth.
• There exists an (at most) countably infinite [math]J \subset I[/math] so that [math]\bigcup_{\alpha \in J} U_\alpha = M[/math], i.e. there exists a countable cover of [math]M[/math].
• Whenever [math]p_1[/math] and [math]p_2[/math] are distinct point in [math]M[/math], there exist [math]U_\alpha[/math] and [math]U_\beta[/math] (not necessarily distinct) so that there exist disjoint sets [math]V \subset U_\alpha[/math] and [math]W \subset U_\beta[/math], with [math]\varphi_\alpha(V)[/math] and [math]\varphi_\beta(W)[/math] open in [math]\mathbb{R}^n[/math], with [math]p_1 \in V[/math] and [math]p_2 \in W[/math].

We say that each pair [math]\left( U_\alpha, \varphi_\alpha \right)[/math] is a (smooth) chart and that the set [math]\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}[/math] is a (smooth) atlas of [math]M[/math]. The maps [math]\tau_{\alpha,\beta} := \varphi_\beta \circ \varphi_\alpha^{-1}[/math] are called the atlas' transition maps. Since the transition maps are from [math]\mathbb{R}^n[/math] to [math]\mathbb{R}^n[/math] we know exactly what it means for these maps to be smooth. Charts that have smooth transition maps both ways are said to be compatible. This construction is illustrated in Fig. figure, for details and proof see .

A manifold [math]M[/math] with two charts [math]\left(U_\alpha, \varphi_\alpha\right)[/math] and [math]\left( U_\beta, \varphi_\beta\right)[/math] and their transitions maps [math]\tau_{\alpha,\beta}[/math] and [math]\tau_{\beta,\alpha}[/math].

[The manifold is not the atlas]

In Lemma lemma we say that the set [math]M[/math] along with an atlas [math]\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}[/math] gives a smooth manifold rather than stating that it is a smooth manifold. This is because we could construct another atlas compatible with the first but the set together with the new atlas would still describe the same manifold. In example example this distinction will be clear as we can see that we can construct any number of atlases describing the same manifold.

We say two atlases are compatible if the transition maps between charts of the two atlases are also smooth, if two atlases are compatible they describe the same manifold. Formally we could define a smooth manifold as the equivalence class of all atlases per Lemma lemma under the equivalence relation of the atlases being compatible.

We could also consider the union of all possible compatible atlases, called the maximal atlas as defining the manifold.

[Hausdorff space]

Item (v) of Lemma lemma guarantees that a manifold is a Hausdorff space, this simply means that for any two distinct points [math]p_1[/math] and [math]p_2[/math] we can find neighborhoods of both that are disjoint (a neighborhood in the manifold being a preimage of a neighborhood in a chart). This may seem redundant but one can construct counterexamples that satisfy (i)-(iv) but not (v). The Hausdorff property is needed for limits to be unique and manifolds are required to be Hausdorff for that reason.

We define what the open subsets of the manifold are by looking at their images in [math]\mathbb{R}^n[/math]. A subset [math]V \subset M[/math] is open if [math]\varphi_\alpha \left( V \cap U_\alpha \right)[/math] is open in [math]\mathbb{R}^n[/math] for all [math]\alpha \in I[/math]. In other words: we let the atlas and the standard topology on [math]\mathbb{R}^n[/math] define the topology of the manifold. With this definition we could rephrase item (v) of Lemma lemma as: for any two distinct points of [math]M[/math] there exist neighborhoods (i.e. open subsets containing the point in question) of said two points that are disjoint. Of course if [math]\left( U_\alpha, \varphi_\alpha \right)[/math] is a chart then if [math]V \subset U_\alpha[/math] is open then [math]\left( V, \varphi_\alpha\vert_V \right)[/math] is also a chart.

[Open sets and continuous charts]

Defining the open sets of [math]M[/math] as the preimages of open subsets of [math]\mathbb{R}^n[/math] makes the charts continuous maps by definition. It might be the case that when we are constructing a manifold we do not start with [math]M[/math] being just a set. For example, in many cases we start with [math]M[/math] being a subset of [math]\mathbb{R}^n[/math], in that case we already know what the open subsets of [math]M[/math] are (i.e. the topology of [math]M[/math] is already known). If we already decided what the open subsets of [math]M[/math] are going to be then we need to make sure that the two notions of `open' coincide. This requires that the charts are continuous maps by construction instead of them being continuous by definition.

Lemma lemma is a characterization so it works the other way around as well. If [math]M[/math] is a smooth manifold then it is always possible to produce a smooth atlas, i.e. a set [math]\left\{ \left( U_\alpha, \varphi_\alpha \right) \right\}_{\alpha \in I}[/math] that satisfies all the conditions of the lemma.

Example [The unit circle]

Let [math]S^1[/math] be the unit circle in [math]\mathbb{R}^2[/math], i.e. [math]S^1 = \left\{ (x,y) \ \middle\vert\ x^2+y^2=1 \right\}[/math]. Then we can construct two smooth charts that cover [math]S^1[/math]:

[[math]] \begin{align*} & U_1 = S^1 \setminus \left\{ \left(-1,0\right) \right\}, \qquad \varphi_1(x,y): U_1 \to (-\pi,\pi), \\ & U_2 = S^1 \setminus \left\{ \left( 1,0 \right) \right\}, \qquad \varphi_2(x,y): U_2 \to (0,2\pi) . \end{align*} [[/math]]

Where [math]\varphi_1[/math] gives the angle between the [math]x[/math]-axis and [math](x,y)[/math] measured from [math]-\pi[/math] to [math]\pi[/math] and [math]\varphi_2[/math] gives that same angle measured from [math]0[/math] to [math]2 \pi[/math], as illustrated in Figure figure. Clearly [math]U_1 \cup U_2 = S^1[/math] and we see that [math]\varphi_1(U_1)=\left(-\pi,\pi\right)[/math] and [math]\varphi_2(U_2)=\left(0,2\pi \right)[/math], so these two charts form an atlas of [math]S^1[/math]. Now we have to check the transition maps, note that [math]U_1 \cap U_2 = S^1 \setminus \left\{ (-1,0), (1,0) \right\}[/math] which consists of two disjoint components, so the transition map from the first to the second chart would have as domain [math](-\pi,0) \cup (0,\pi)[/math] and be defined as:

[[math]] \begin{equation*} \tau_{1,2} (\theta) = \varphi_2 \circ \varphi_1^{-1} (\theta) = \begin{cases} \theta & \text{ if } \theta \in (0,\pi), \\ \theta + 2 \pi & \text{ if } \theta \in (-\pi,0), \end{cases} \end{equation*} [[/math]]

which is smooth on its domain (the discontinuity at [math]\theta=0[/math] is not part of the domain). The inverted transition map is similarly smooth. The whole construction is visualized in Fig. figure.

A smooth atlas on [math]S^1[/math] with the transition maps illustrated in grey.

Smooth Maps

An important reason for introducing smooth manifolds is being able to talk about smooth maps. While the terms map and function are technically interchangeable we will use the term function for maps whose co-domain is [math]\mathbb{R}[/math] or [math]\mathbb{R}^k[/math] and use map for more general maps between manifolds.

Definition (Smooth map)

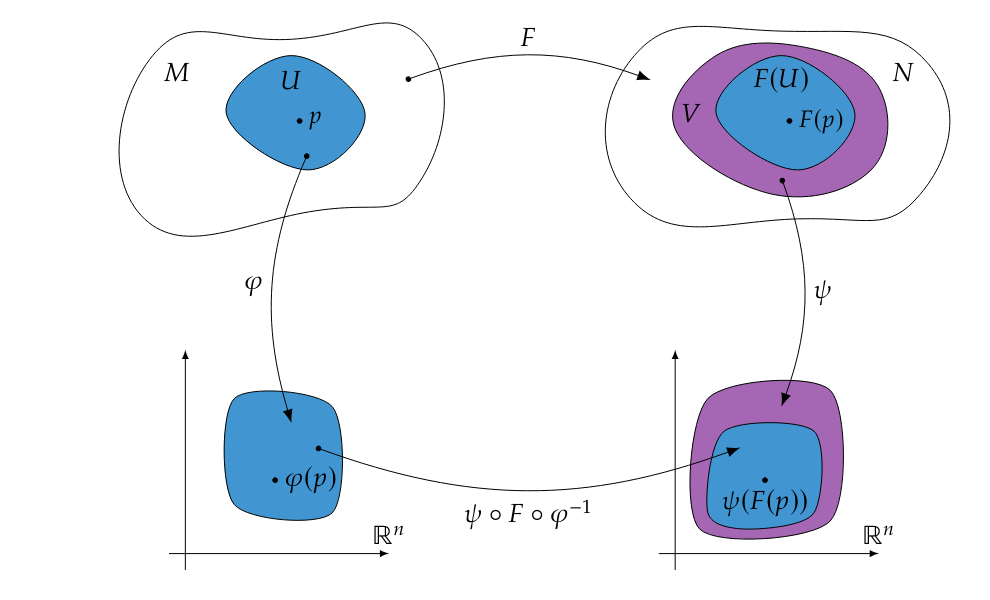
Let [math]M[/math] and [math]N[/math] be two smooth manifolds and let [math]F:M \to N[/math] be any map. We say [math]F[/math] is a smooth map if for every [math]p \in M[/math] there exists a smooth chart [math]\left( U, \varphi \right)[/math] of [math]M[/math] that contains [math]p[/math] and a smooth chart [math]\left( V, \psi \right)[/math] of [math]N[/math] that contains [math]F(p)[/math] so that [math]F(U) \subseteq V[/math] and the map [math]\psi \circ F \circ \varphi^{-1}[/math] is smooth from [math]\varphi(U)[/math] to [math]\psi(F(U)) \subseteq \psi(V)[/math].

Due to the smooth structure (i.e. all of its possible atlases) that a smooth manifold is equipped with this definition is independent of the choice of charts, the smoothness of transition maps ensures this key property. The definition makes it clear that we can only talk about the smoothness of maps if the manifolds in question have smooth structures, so when we say [math]F:M\to N[/math] is a smooth map we imply that [math]M[/math] and [math]N[/math] are smooth manifolds even if we do not specify that fact explicitly. The construction from the definition is illustrated in Fig. figure.

A smooth map [math]F[/math] between two manifolds and its representation [math]\psi \circ F \circ \varphi^{-1}[/math] between chart co-domains.

With smooth function we now just mean a smooth map from [math]M[/math] to [math]\mathbb{R}[/math] or [math]\mathbb{R}^k[/math]. Another special case for which we reserve its own term is that of a smooth curve: a smooth map from [math]\mathbb{R}[/math] (or some interval of [math]\mathbb{R}[/math]) to another smooth manifold. Example

The map [math]F:\mathbb{R} \to S^1[/math] given by [math]F(\theta):=\left( \cos\theta,\, \sin\theta \right)[/math] is a smooth map from the manifold [math]\mathbb{R}[/math] to the manifold [math]S^1[/math].

Definition (Diffeomorphism)

Let [math]M[/math] and [math]N[/math] be smooth manifolds, a smooth bijective map from [math]M[/math] to [math]N[/math] that has a smooth inverse is called a diffeomorphism. Two manifolds between which a diffeomorphism exists are said to be diffeomorphic.

Example

The unit circle [math]S^1[/math] is not diffeomorphic with [math]\mathbb{R}[/math] since there exists no continuous bijection between the two.

The unit circle is however diffeomorphic with the group [math]\iident{SO}(2)[/math] (i.e. the group of orthogonal [math]2 \times 2[/math] matrices with determinant 1) via the identification

[[math]] \begin{equation*} S^1 \ni (x,y) \leftrightarrow \begin{bmatrix} x & -y \\ y & x \end{bmatrix} \in \iident{SO}(2) , \end{equation*} [[/math]]

usually parametrized with [math]\theta \in \mathbb{R}/(2\pi\mathbb{Z})[/math] as

[[math]] \begin{equation*} S^1 \ni (\cos\theta,\sin\theta) \leftrightarrow \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \in \iident{SO}(2) . \end{equation*} [[/math]]

General references

Smets, Bart M. N. (2024). "Mathematics of Neural Networks". arXiv:2403.04807 [cs.LG].