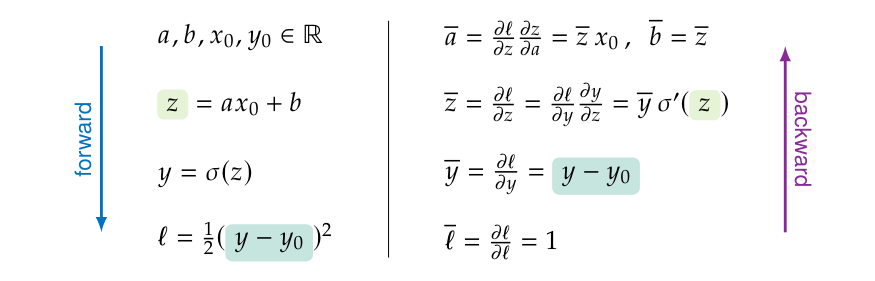Automatic Differentiation & Backpropagation

[math] \newcommand{\ul}{\mathbf} \newcommand{\symbf}{\bm} \newcommand\subsetap{\mathrel{\overset{\makebox[0pt]{\mbox{\normalfont\tiny\sffamily ap.}}}{\rule{0pt}{.8ex}\smash{\subset}}}} \newcommand{\rident}[1]{\mathrm{#1}} \newcommand{\iident}[1]{\mathit{#1}} \newcommand{\wip}{\emoji{construction}} \newcommand{\pointright}{\emoji{backhand-index-pointing-right-light-skin-tone}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\Arg}{Arg} \DeclareMathOperator*{\Var}{Var} \DeclareMathOperator*{\dom}{dom} \DeclareMathOperator{\Div}{div} \DeclareMathOperator{\morph}{\scalebox{0.7}{\ensuremath\square}} \DeclareMathOperator*{\esssup}{ess\,sup} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Cl}{Cl} \DeclareMathOperator{\id}{id} \DeclareMathOperator{\diam}{diam} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\arctantwo}{arctan2} \DeclareMathOperator{\relu}{ReLU} \newcommand{\mathds}{\mathbb}[/math]

This article was automatically generated from a tex file and may contain conversion errors. If permitted, you may login and edit this article to improve the conversion.

All our training algorithms are gradient based and so our ability to train a network rests on us computing those gradients. The traditional approaches we could take are:

• compute the derivative formulas ourselves and code them into the program,
• use a computer algebra system to perform symbolic differentiation and use the resulting formula,
• use numeric differentiation (i.e. finite differences).

None of these three options are appealing. We definitely do not want to work out the derivatives ourselves for every network we define so option (1) is out. Symbolic differentiation with computer algebra systems like Mathematica usually produces complex and cryptic expressions in non-trivial cases. Subsequently evaluating these complex expressions is usually anything but efficient, this rules out option (2). For networks with millions if not billions of parameters computing finite differences would entail millions or billions of evaluations of the network, this makes option (3) impossible to use.

What we need is a fourth technique: automatic differentiation, also called algorithmic differentiation or simply autodiff. We will restrict ourselves to looking at automatic differentiation in the context of feed-forward neural networks but it is a very general technique, see for a broader survey of its uses in machine learning. In introducing automatic differentiation it is perhaps best to emphasizing that it is not symbolic differentiation nor numeric differentiation, even though it contains elements of both.

[Autograd vs. autodiff]

Autograd is a particular autodiff implementation in Python. Autograd served as a prototype for a lot of autodiff implementations, including PyTorch's, for that reason in PyTorch the term autograd is used as a synonym for autodiff.

Notation and an Example

Let us say we have a network [math]F:\mathbb{R}\times \mathbb{R}^2 \to \mathbb{R}[/math] with two parameters [math]a[/math] and [math]b[/math] and loss function [math]\ell[/math]. We are interested in computing:

[[math]] \begin{equation} \label{eq:a_b_derivatives} \left. \frac{\partial}{\partial a}\ell(F(x_0;a,b),y_0) \right\vert_{(a,b)} \quad \text{and} \quad \left. \frac{\partial}{\partial b}\ell(F(x_0;a,b),y_0) \right\vert_{(a,b)} , \end{equation} [[/math]]

i.e. the partial derivatives with respect to out parameters at their current values which are just real numbers. Note how we use [math]a[/math] and [math]b[/math] first as dummy variables to indicate the input we want to differentiate over and then again as real valued function arguments.

Partial derivative notation can get cluttered quickly, as \ref{eq:a_b_derivatives} shows. To simplify things we are going to introduce some notational conventions. Let [math]f:\mathbb{R}^2 \to \mathbb{R}[/math] be given by

[[math]] \begin{equation} \label{eq:fghk} f(x,y) = g(h(x,y),k(x,y)) , \end{equation} [[/math]]

where [math]g,h[/math] and [math]k[/math] are also functions from [math]\mathbb{R}^2[/math] to [math]\mathbb{R}[/math]. We evaluate [math]f[/math] at a fixed [math](x,y)[/math] by calculating:

[[math]] \begin{equation*} u = h(x,y) , \quad v = k(x,y) , \quad z = g(u,v) = f(x,y) , \end{equation*} [[/math]]

which are all just real numbers and not functions like [math]f,g,h[/math] and [math]k[/math] are. Now we introduce the following notations for the intermediate results [math]u[/math] and [math]v[/math]:

[[math]] \begin{equation*} \begin{split} \frac{\partial u}{\partial x} &:= \left. \frac{\partial}{\partial x} h(x,y) \right|_{(x,y)} , \qquad \frac{\partial u}{\partial y} := \left. \frac{\partial}{\partial y} h(x,y) \right|_{(x,y)} , \\ \frac{\partial v}{\partial x} &:= \left. \frac{\partial}{\partial x} k(x,y) \right|_{(x,y)} , \qquad \frac{\partial v}{\partial y} := \left. \frac{\partial}{\partial y} k(x,y) \right|_{(x,y)} , \end{split} \end{equation*} [[/math]]

and for the final output [math]z[/math] we define:

[[math]] \begin{equation*} \begin{split} \frac{\partial z}{\partial u} &:= \left. \frac{\partial}{\partial u} g(u,v) \right|_{(u,v)} , \qquad \frac{\partial z}{\partial v} := \left. \frac{\partial}{\partial v} g(u,v) \right|_{(u,v)} \\ \frac{\partial z}{\partial x} &:= \left. \frac{\partial}{\partial x} f(x,y) \right|_{(x,y)} , \qquad \frac{\partial z}{\partial y} := \left. \frac{\partial}{\partial y} f(x,y) \right|_{(x,y)} , \end{split} \end{equation*} [[/math]]

which are all real numbers. At first glance the partial derivative of one real number with respect to another real number is nonsensical, but if we use one real number in the computation of a second one it does make sense to ask how sensitive the value of the second is with respect to the first if we changed it a little bit. This sensitivity is of course nothing but the partial derivative of the function used in the computation of the second value evaluated at the first value. But since we are not interested in the whole partial derivatives it simplifies things to keep the function and its partial derivatives implicit and use the simpler notation we just introduced.

Using this notation the chain rule applied to \ref{eq:fghk} can be expressed very succinctly as

[[math]] \begin{equation} \label{eq:numeric_chain_rule} \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial x} \quad \text{and} \quad \frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \frac{\partial v}{\partial y} . \end{equation} [[/math]]

We are always looking to minimize our chosen loss function, hence we are mainly interested in the partial derivatives of the loss function. We will use the following notation to further abbreviate the partial derivatives of the loss: let [math]\ell \in \mathbb{R}[/math] be the loss produced at the end of our calculation and let [math]\alpha \in \mathbb{R}[/math] be either a parameter or intermediate result used in the calculation of [math]\ell[/math] then we write

[[math]] \begin{equation*} \overline{\alpha} := \frac{\partial \ell}{\partial \alpha} , \end{equation*} [[/math]]

which we refer to as a gradient (technically the value of the gradient of the loss function with respect to [math]\alpha[/math] evaluated at the current value of [math]\alpha[/math], but that is quite the mouthful). So in the case of the two-parameter network [math]F[/math] from before: for a given set of parameters [math]a,b \in \mathbb{R}[/math] we need to calculate the gradients [math]\overline{a},\overline{b} \in \mathbb{R}[/math], which are exactly the evaluated partial derivatives from \ref{eq:a_b_derivatives}. As an example to see how this notation works let us pick a concrete example and systematically work through differentiating it. Let [math]F(x;a,b):=\sigma(a x + b)[/math] for some choice of (differentiable) activation function [math]\sigma:\mathbb{R} \to \mathbb{R}[/math]. Let [math](x_0,y_0) \in \mathbb{R}^2[/math] be some data point and let us use the loss function [math](y,y') \mapsto \frac{1}{2}(y-y')^2[/math]. After we pick our parameter values [math]a,b \in \mathbb{R}[/math] we can simply compute the corresponding loss, doing this is called the forward pass and is shown on the left side in equation below.

After having evaluated the network we can start calculating the partial derivatives of the loss with respect the the parameters [math]a[/math] and [math]b[/math] by apply the chain rule from back to front, this is called the backward pass and is shown on the right side in equation. Some thing to note about the schematic in equation.

• Everything that we wrote down is a numeric computation and the whole schematic can be executed by a computer as is.
• In writing down the backward pass we did use our symbolic knowledge of how the operations in the forward pass need to be differentiated if we look at them as functions.
• Writing down the trivial [math]\overline{\ell}=1[/math] is of course redundant, but autodiff implementations such as PyTorch's do actually start the backward pass by creating a single element tensor containing the value [math]1[/math] (and it makes the schematic look symmetric).
• Some of the intermediate values computed during the forward pass are reused during the backward pass. In the schematic equation the reused values have been shaded in green.

In PyTorch, the intermediate results computed during the forward pass that need to be retained for the backward pass are called saved tensors. In a typical neural network many of the intermediate results have to be saved for the backward pass, this is the reason that training a neural network requires a lot of memory.

Nothing we have done in the example in equation is novel, we just did what we would normally do if asked to calculate these partial derivatives. Only, we wrote it down systematically in a way that we can automate.

Automation & the Computational Graph

The key to automating the type of calculation in equation and equation is splitting it into primitive operations and tracking how they are composed. Consider the network [math]F(x;a,b):=\relu(a x + b)[/math] with loss function [math](y,y')\mapsto \frac{1}{2}(y-y')^2[/math] evaluated for some data point [math](x_0,y_0) \in \mathbb{R}^2[/math] and parameter values [math]a,b \in \mathbb{R}[/math]. Evaluating the network one primitive operation at a time looks as follows.

The backward pass consists again of numeric computations but at every step we need to know how the value computed at that line, say [math]\alpha[/math], is used so we are able to compute the correct partial derivative [math]\overline{\alpha}[/math]. In the case of equation that is fairly straightforward as every intermediate value is only used in the next step i.e. [math]t_i[/math] only depend on [math]t_{i-1}[/math] and the parameters. Consequently [math]\overline{t_i}[/math] only depends on [math]\overline{t_{i+1}}[/math] and [math]t_i[/math]. A more general example that has a slightly more complicated structure is the network [math]F(x;a,b):=\relu(a x + b) + (a x + b)[/math]. We can write this network out in primitive form as well, we omit the forward/backward arrows but add a dependency graph that shows how the intermediate results depend on each other.

The dependency graph of the gradients [math]\overline{t_i}[/math] in equation is naturally the reverse of the dependency graph of the values [math]t_i[/math] augmented with dependencies on the results from the forward pass. Both the values [math]t_3[/math] and [math]t_4[/math] depend on the value [math]t_2[/math] hence [math]\overline{t_2}[/math] depends on both [math]\overline{t_3}[/math] and [math]\overline{t_4}[/math] in addition to [math]t_2[/math] itself. This double dependency causes the chain rule applied to [math]\overline{t_2}[/math] to have two terms, of course this generalizes to multiple dependencies. Constructing this computational graph is exactly how machine learning frameworks such as PyTorch implement gradient computation. Each time you perform an operation on one or more tensors a new node is added to the graph to record what operation was performed and on which inputs the output depends. Then, when it becomes time to compute the gradient (i.e. R is called in PyTorch) the graph is traversed back to front. As mentioned, the graph records what operation was performed at each node. This is necessary because what backward computation needs to be performed at each node depends on what the corresponding forward computation was, this is where our symbolic knowledge needs to be added.

Implementing Operations

In the previous section we saw how the evaluation of a neural network (or any computation for that matter) can be expressed as a computational graph where each node correspond to a (primitive) operation. To be able to do the backward pass each node needs to know how to compute its own partial derivative(s). Previous examples equation equation and equation only used simple scalar operations, now will explore how to implement both the forward and backward computation for a general multivariate vector-valued function. Let [math]F:\mathbb{R}^n \to \mathbb{R}^m[/math] be a differentiable map, let [math]\boldsymbol{x}=[x_1 \ \cdots \ x_n]^T \in \mathbb{R}^n[/math] and [math]\boldsymbol{y}=[y_1 \ \cdots \ y_m]^T \in \mathbb{R}^m[/math] so that [math]\boldsymbol{y}=F(\boldsymbol{x})[/math]. Let [math]\ell \in \mathbb{R}[/math] be the final loss computed for a neural network that contains [math]F[/math] as one of its operations. Then we can generalize our gradient notation from scalars to vector as

[[math]] \begin{equation*} \overline{\boldsymbol{x}} := \frac{\partial \ell}{\partial \boldsymbol{x}} := \begin{bmatrix} \frac{\partial \ell}{\partial x_1} \\ \vdots \\ \frac{\partial \ell}{\partial x_n} \end{bmatrix} , \qquad \overline{\boldsymbol{y}} := \frac{\partial \ell}{\partial \boldsymbol{y}} := \begin{bmatrix} \frac{\partial \ell}{\partial y_1} \\ \vdots \\ \frac{\partial \ell}{\partial y_m} \end{bmatrix} . \end{equation*} [[/math]]

During the forward pass the task is: given [math]\boldsymbol{x}[/math] compute [math]\boldsymbol{y}=F(\boldsymbol{x})[/math]. During the the backward pass the task is: given [math]\boldsymbol{x}[/math] and [math]\overline{\boldsymbol{y}}[/math] compute [math]\overline{\boldsymbol{x}}[/math], we call this backward operation [math]\overline{F}:\mathbb{R}^n \times \mathbb{R}^m \to \mathbb{R}^n[/math]. Let us see what it looks like

[[math]] \begin{align*} \overline{\boldsymbol{x}} &= \begin{bmatrix} \frac{\partial \ell}{\partial x_1} \\ \vdots \\ \frac{\partial \ell}{\partial x_n} \end{bmatrix} \\ &= \begin{bmatrix} \sum_{j=1}^m \frac{\partial \ell}{\partial y_j} \frac{\partial y_j}{\partial x_1} \\ \vdots \\ \sum_{j=1}^m \frac{\partial \ell}{\partial y_j} \frac{\partial y_j}{\partial x_n} \end{bmatrix} \\ &= \begin{bmatrix} \sum_{j=1}^m \overline{y_j} \, \frac{\partial y_j}{\partial x_1} \\ \vdots \\ \sum_{j=1}^m \overline{y_j} \, \frac{\partial y_j}{\partial x_n} \end{bmatrix} \\ &= \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_1} \\ \vdots & & \vdots \\ \frac{\partial y_1}{\partial x_n} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \begin{bmatrix} \overline{y_1} \vphantom{\frac{\partial y_1}{\partial x_1}} \\ \vdots \\ \overline{y_m} \vphantom{\frac{\partial y_1}{\partial x_1}} \end{bmatrix} \\ &= J(\boldsymbol{x})^T \overline{\boldsymbol{y}} , \end{align*} [[/math]]

where [math]J(\boldsymbol{x})[/math] is the Jacobian matrix of [math]F[/math] evaluated in [math]\boldsymbol{x}[/math]. So not unexpectedly we end up with the general form of the chain rule. Example [Pointwise addition] Let [math]F:\mathbb{R}^2 \times \mathbb{R}^2 \to \mathbb{R}^2[/math] be defined by [math]F(\boldsymbol{a},\boldsymbol{b}) := \boldsymbol{a} + \boldsymbol{b}[/math], with [math]\boldsymbol{a}=[a_1 \ a_2]^T \in \mathbb{R}^2[/math] and [math]\boldsymbol{b}=[b_1 \ b_2]^T[/math]. We can equivalently define [math]F[/math] as [math]F:\mathbb{R}^4 \to \mathbb{R}^2[/math] as follows:

[[math]] \begin{equation*} \boldsymbol{c} = F(\boldsymbol{a},\boldsymbol{b}) = \begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ b_1 \\ b_2 \end{bmatrix} = \begin{bmatrix} a_1 + b_1 \\ a_2 + b_2 \end{bmatrix} . \end{equation*} [[/math]]

Since this is a linear operator the Jacobian matrix is just the constant matrix above. The backward operation [math]\overline{F}:\mathbb{R}^4 \times \mathbb{R}^2 \to \mathbb{R}^4[/math] is then given by

[[math]] \begin{equation*} \begin{bmatrix} \overline{\boldsymbol{a}} \\ \overline{\boldsymbol{b}} \end{bmatrix} = \overline{F}(\boldsymbol{a},\boldsymbol{b},\overline{\boldsymbol{c}}) = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} \overline{c_1} \\ \overline{c_2} \end{bmatrix} = \begin{bmatrix} \overline{c_1} \\ \overline{c_2} \\ \overline{c_1} \\ \overline{c_2} \end{bmatrix} = \begin{bmatrix} \overline{\boldsymbol{c}} \\ \overline{\boldsymbol{c}} \end{bmatrix} \end{equation*} [[/math]]

for a gradient [math]\overline{\boldsymbol{c}} = [c_1 \ c_2]^T \in \mathbb{R}^2[/math].

So to implement this operation we do not have to retain the inputs [math]\boldsymbol{a}[/math] and [math]\boldsymbol{b}[/math], we can implement the backward calculation by simply copying the incoming gradient [math]\overline{\boldsymbol{c}}[/math] and passing the two copies up the graph.

Example [Copy] Let [math]F:\mathbb{R}^n \to \mathbb{R}^{2n}[/math] be given by

[[math]] \begin{equation*} \begin{bmatrix} \boldsymbol{b} \\[4pt] \boldsymbol{c} \end{bmatrix} = F(\boldsymbol{a}) = \begin{bmatrix} a_1 \\ \vdots \\ a_n \\[2pt] a_1 \\ \vdots \\ a_n \end{bmatrix} , \end{equation*} [[/math]]

with [math]\boldsymbol{a},\boldsymbol{b},\boldsymbol{c} \in \mathbb{R}^n[/math]. This operation makes two copies of its input, it is clearly linear with Jacobian

[[math]] \begin{equation*} J = \begin{bmatrix} I_n \\[4pt] I_n \end{bmatrix} , \end{equation*} [[/math]]

where [math]I_n[/math] is a unit matrix of size [math]n \times n[/math]. Given gradients [math]\overline{\boldsymbol{b}},\overline{\boldsymbol{c}} \in \mathbb{R}^n[/math] of the outputs the gradient [math]\overline{\boldsymbol{a}}[/math] of the input is calculated as:

[[math]] \begin{equation*} \overline{\boldsymbol{a}} = \overline{F}(\boldsymbol{a},\overline{\boldsymbol{b}},\overline{\boldsymbol{c}}) = \begin{bmatrix} I_n & I_n \end{bmatrix} \begin{bmatrix} \overline{\boldsymbol{b}} \\[4pt] \overline{\boldsymbol{c}} \end{bmatrix} = \overline{\boldsymbol{b}} + \overline{\boldsymbol{c}} . \end{equation*} [[/math]]

Example [Inner product] In this example the Jacobian is not constant and we do have to retain the inputs to be able to do the backward pass. Let [math]F:\mathbb{R}^{2n} \to \mathbb{R}[/math] be given by

[[math]] \begin{equation*} c = F(\boldsymbol{a},\boldsymbol{b}) = \sum_{i=1}^n a_i b_i , \end{equation*} [[/math]]

for [math]\boldsymbol{a}=[a_1 \ \cdots\ a_n]^T[/math] and [math]\boldsymbol{b}=[b_1 \ \cdots\ b_n]^T \in \mathbb{R}^n[/math]. Then the Jacobian matrix evaluated at [math][\boldsymbol{a} \ \boldsymbol{b}]^T[/math] is given by

[[math]] \begin{equation*} J(\boldsymbol{a},\boldsymbol{b}) = \begin{bmatrix} b_1 & \cdots & b_n & a_1 & \cdots & a_n \end{bmatrix} = \begin{bmatrix} \boldsymbol{b}^T & \boldsymbol{a}^T \end{bmatrix} . \end{equation*} [[/math]]

Given a (scalar) gradient [math]\overline{c} \in \mathbb{R}[/math] of the output we compute the gradients of [math]\boldsymbol{a}[/math] and [math]\boldsymbol{b}[/math] as follows:

[[math]] \begin{equation*} \begin{bmatrix} \overline{\boldsymbol{a}} \\[4pt] \overline{\boldsymbol{b}} \end{bmatrix} = \overline{F}(\boldsymbol{a},\boldsymbol{b},\overline{c}) = \begin{bmatrix} \boldsymbol{b}^T & \boldsymbol{a}^T \end{bmatrix}^T \, \overline{c} = \overline{c} \, \begin{bmatrix} \boldsymbol{b} \\[4pt] \boldsymbol{a} \end{bmatrix} , \end{equation*} [[/math]]

which depends on the input values [math]\boldsymbol{a}[/math] and [math]\boldsymbol{b}[/math].

In equation and equation we deconstructed the loss function [math](y,y') \mapsto \frac{1}{2}(y-y')^2[/math] into three primitive operations. As a consequence the backward pass has a step where we first multiply with [math]2[/math] and then multiply with [math]\frac{1}{2}[/math], this is not efficient of course. Hence deconstructing our calculation into the smallest possible operations is not always advisable. In this example we will express the [math]L^2[/math] loss function as single operation instead.

Example [[math]L^2[/math] loss] Let [math]F:\mathbb{R}^{2n} \to \mathbb{R}[/math] be given by

[[math]] \begin{equation*} \ell = F(\boldsymbol{y},\boldsymbol{y}') = \frac{1}{2} \sum_{i=1}^{n} (y_i - y_i')^2 \end{equation*} [[/math]]

for [math]\boldsymbol{y}=[y_1 \ \cdots\ y_n]^T[/math] and [math]\boldsymbol{y}'=[y_1' \ \cdots\ y_n']^T \in \mathbb{R}^n[/math]. Then the Jacobian matrix evaluated at [math][\boldsymbol{y} \ \boldsymbol{y}']^T[/math] is given by

[[math]] \begin{equation*} J(\boldsymbol{y},\boldsymbol{y}') = \begin{bmatrix} y_1 - y_1' & \cdots & y_n - y_n' & y_1'-y_1 & \cdots & y_n'-y_n \end{bmatrix} = \begin{bmatrix} (\boldsymbol{y}-\boldsymbol{y}')^T & (\boldsymbol{y}'-\boldsymbol{y})^T \end{bmatrix} . \end{equation*} [[/math]]

The backward operation has signature [math]\overline{F}:\mathbb{R}^{2n} \times \mathbb{R} \to \mathbb{R}^{2n}[/math]. The second argument of [math]\overline{F}[/math] is a given gradient [math]\overline{\ell} \in \mathbb{R}[/math], which is trivially [math]\overline{\ell}=1[/math] if the output [math]\ell[/math] is the final loss we are interested in minimizing. We then compute the gradients as follows:

[[math]] \begin{equation*} \begin{bmatrix} \overline{\boldsymbol{y}} \\[4pt] \overline{\boldsymbol{y}'} \end{bmatrix} = \overline{F}(\boldsymbol{y},\boldsymbol{y}',\overline{\ell}=1) = \begin{bmatrix} (\boldsymbol{y}-\boldsymbol{y}')^T & (\boldsymbol{y}'-\boldsymbol{y})^T \end{bmatrix}^T \, \overline{\ell} = \begin{bmatrix} \boldsymbol{y}-\boldsymbol{y}' \\[4pt] \boldsymbol{y}'-\boldsymbol{y} \end{bmatrix} . \end{equation*} [[/math]]

If [math]\boldsymbol{y}[/math] is the output of the neural network and [math]\boldsymbol{y}'[/math] is the data point then we are only interested in [math]\overline{\boldsymbol{y}}[/math] and we would only compute [math]\boldsymbol{y}-\boldsymbol{y}'[/math]. This is equivalent to the computation in equation and equation but avoids the redundant multiplications.

General references

Smets, Bart M. N. (2024). "Mathematics of Neural Networks". arXiv:2403.04807 [cs.LG].