Lie Groups

[math] \newcommand{\ul}{\mathbf} \newcommand{\symbf}{\bm} \newcommand\subsetap{\mathrel{\overset{\makebox[0pt]{\mbox{\normalfont\tiny\sffamily ap.}}}{\rule{0pt}{.8ex}\smash{\subset}}}} \newcommand{\rident}[1]{\mathrm{#1}} \newcommand{\iident}[1]{\mathit{#1}} \newcommand{\wip}{\emoji{construction}} \newcommand{\pointright}{\emoji{backhand-index-pointing-right-light-skin-tone}} \DeclareMathOperator*{\argmax}{arg\,max} \DeclareMathOperator*{\argmin}{arg\,min} \DeclareMathOperator*{\Arg}{Arg} \DeclareMathOperator*{\Var}{Var} \DeclareMathOperator*{\dom}{dom} \DeclareMathOperator{\Div}{div} \DeclareMathOperator{\morph}{\scalebox{0.7}{\ensuremath\square}} \DeclareMathOperator*{\esssup}{ess\,sup} \DeclareMathOperator{\Int}{Int} \DeclareMathOperator{\Cl}{Cl} \DeclareMathOperator{\id}{id} \DeclareMathOperator{\diam}{diam} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\arctantwo}{arctan2} \DeclareMathOperator{\relu}{ReLU} \newcommand{\mathds}{\mathbb}[/math]

This article was automatically generated from a tex file and may contain conversion errors. If permitted, you may login and edit this article to improve the conversion.

Basic Definitions

We assume that the transformations we are interested in form Lie groups. Classical groups such as the general and special linear groups (the groups of matrices that are invertible resp. have determinant 1), the orthogonal group (the group of orthogonal matrices), etc. are examples of Lie groups.

Definition

A Lie group G is a smooth manifold so that G is also an algebraic group given by two smooth maps, one for the group product (also called multiplication):

[[math]] \begin{equation*} G \times G \to G, \quad (g_1,g_2) \mapsto g_1 g_2, \end{equation*} [[/math]]

and one for inversion:

[[math]] \begin{equation*} G \to G, \qquad\quad g \mapsto g^{-1}. \end{equation*} [[/math]]

Recall that being a group, a Lie group has the following properties.

• Closure: [math]\forall g_1, g_2 \in G: g_1 g_2 \in G.[/math]
• Associativity: [math]\forall g_1,g_2,g_3 \in G: (g_1 g_2) g_3=g_1 (g_2 g_3)[/math].
• Unit element: [math]\exists e \in G, \forall g \in G: e g=g e=g[/math] and this element [math]e[/math] is unique. We use the traditional [math]e[/math] to denote the unit element, which derives from the German Einselement.
• Inverse: [math]\forall g \in G \ \exists g^{-1} \in G: gg^{-1}=g^{-1}g=e[/math].

We should emphasize that a group need not be commutative, indeed the particular Lie groups we are most interested in are not commutative and have group elements [math]g_1,g_2[/math] for which [math]g_1 g_2 \neq g_2 g_1[/math]. For [math]g \in G[/math], we denote by [math]L_g:G \to G[/math], [math]L_g(h)=gh[/math] the left multiplication by [math]g[/math] and by [math]R_g:G \to G[/math], [math]R_g(h)=hg[/math] the right multiplication by [math]g[/math]. Left and right multiplication are also sometimes called left and right translation.

Example [math]\mathbb{R}^n[/math] is a (commutative) Lie group under vector addition [math](\boldsymbol{x},\boldsymbol{y})\mapsto \boldsymbol{x}+\boldsymbol{y}[/math] and negation [math]\boldsymbol{x} \mapsto -\boldsymbol{x}[/math].

Example [Multiplicative group of positive real numbers] [math]\mathbb{R}_{ \gt 0}[/math] is a (commutative) Lie group under multiplication [math](x,y) \mapsto x y[/math] and inversion [math]x \mapsto \frac{1}{x}[/math].

Example [General linear group] The general linear group of degree [math]n[/math], [math]\iident{GL}(n)[/math], is the group of all invertible [math]n \times n[/math] matrices. The group product is the matrix product.

Example [Special orthogonal group] The special orthogonal group of degree [math]n[/math], [math]\iident{SO}(n)[/math], is the subgroup of [math]\iident{GL}(n)[/math] of all matrices with determinant [math]1[/math]. It is the group of rotations in [math]n[/math] dimensions. For [math]SO(2)[/math] we write the matrices in terms of the angle of the rotation [math]\theta \in \mathbb{R}/(2\pi\mathbb{Z})[/math] as

[[math]] \begin{equation} \label{eq:so2_matrix} R(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} , \end{equation} [[/math]]

with the group law given by [math]R(\theta_1) R(\theta_2)=R(\theta_1 + \theta_2)[/math].

Example [Special Euclidean group]

The special Euclidean group of degree [math]n[/math], [math]\iident{SE}(n)[/math], is the group of rotations and translations in [math]n[/math] dimensions. As a set it equals [math]\mathbb{R}^n \times \iident{SO}(n)[/math] with the group law given by:

[[math]] \begin{equation} \label{eq:se_law} \left( \boldsymbol{x}_1, R_1 \right) \left( \boldsymbol{x}_2, R_2 \right) = \left( \boldsymbol{x}_1 + R_1 \boldsymbol{x}_2,\, R_1 R_2 \right) . \end{equation} [[/math]]

The group law is not the direct product (i.e. not [math]\left( \boldsymbol{x}_1 + \boldsymbol{x}_2,\, R_1 R_2 \right)[/math]) but the second group affects the law of the first group. We call this a semidirect product, to emphasize this difference we write [math]\iident{SE}(n)=\mathbb{R}^n \rtimes \iident{SO}(n)[/math].

Since we want to design a neural network that takes in 2D images and is rotation-translation equivariant, the Lie group [math]\iident{SE}(2)[/math] is of special interest to us. In the [math]\iident{SE}(2)[/math] case we can either represent elements as [math](\boldsymbol{x},R(\theta)) \in \mathbb{R}^2 \times \iident{SO}(2)[/math] with [math]R(\theta)[/math] the rotation matrix from \ref{eq:so2_matrix}, or as [math](\boldsymbol{x},\theta) \in \mathbb{R}^2 \times [0,2\pi)[/math]. In the latter case the group law can be written as

[[math]] \begin{equation*} (\boldsymbol{x}_1,\theta_1) (\boldsymbol{x}_2,\theta_2) = \left( \boldsymbol{x}_1 + R(\theta_1) \boldsymbol{x}_2 ,\, \theta_1 + \theta_2 \bmod{2\pi} \right) . \end{equation*} [[/math]]

Lie Subgroups

Algebraic groups can have subgroups (think of the many subgroups of the general linear group). Lie groups also have subgroups but those subgroups are not automatically Lie groups themselves. Let [math]G[/math] be a Lie group, then [math]H \subset G[/math] is a Lie subgroup of [math]G[/math] if

• [math]H[/math] is a subgroup of the group [math]G[/math],
• [math]H[/math] is an immersed submanifold of the manifold [math]G[/math],
• the group operations on [math]H[/math] are smooth.

We have not seen what an immersed submanifold is and this is beyond the scope of this course. However the following theorem provides an easier way of identifying most Lie subgroups.

Theorem (Cartan’s closed subgroup theorem)

Any subgroup of a Lie group that is closed (as a set) is a Lie subgroup.

See for proof and details. Not all Lie subgroups are closed but the ones we are interested in all are. Consequently Theorem theorem is our go-to method for proving whether a subgroup is a Lie group.

Example

Every linear subspace of [math]\mathbb{R}^n[/math] is a (closed) Lie subgroup under vector addition.

Example

The groups [math]\mathbb{R}^n \times \{ 0 \}[/math] and [math]\{ \boldsymbol{0} \} \times \iident{SO}(n)[/math] are (closed) Lie subgroups of [math]\iident{SE}(n)[/math].

Group Actions

The most important use of Lie groups in manifold theory involves the action of a Lie group on a manifold.

Definition (Group action)

If [math]G[/math] is a group and [math]M[/math] a set then a left action of [math]G[/math] on [math]M[/math] is a map [math]G \times M \to M[/math] written as [math](g,p) \mapsto g \cdot p[/math] that satisfies:

[[math]] \begin{equation} \begin{alignedat}{2} g_2 \cdot (g_1 \cdot p) &= (g_2 g_1) \cdot p \qquad &&\forall g_1,g_2 \in G, p \in M, \\ e \cdot p &= p && \forall p \in M. \end{alignedat} \label{eq:left_action} \end{equation} [[/math]]

A right action is defined similarly as a map [math]M \times G \to M[/math] that satisfies:

[[math]] \begin{equation*} \begin{alignedat}{2} (p \cdot g_1) \cdot g_2 &= p \cdot (g_1 g_2) \qquad &&\forall g_1,g_2 \in G, p \in M, \\ p \cdot e &= p && \forall p \in M. \end{alignedat} \end{equation*} [[/math]]

If both [math]G[/math] and [math]M[/math] are manifolds and the map is smooth in both inputs [math]G[/math] and [math]M[/math] then we say the action is a smooth action.

We will focus exclusively on left actions since their group law \ref{eq:left_action} has the property that group multiplication corresponds to map composition. In any case a right action can always be converted to a left action by defining [math]g \cdot p := p \cdot g^{-1}[/math], or vice versa for turning a left action into a right action. In our setting [math]G[/math] is always a Lie group and [math]M[/math] always a manifold and we will only be considering smooth actions. Sometimes it is convenient to label an action, say [math]\rho:G \times M \to M[/math]. The action of a group element [math]g[/math] on a point [math]p[/math] can then be written equivalently as [math]g \cdot p \equiv \rho(g,p) \equiv \rho_g(p)[/math]. If [math]\rho[/math] is a smooth action then for all [math]g \in G[/math], [math]\rho_g : M \to M[/math] is a diffeomorphism since [math]\rho_{g^{-1}}[/math] is a smooth inverse. A group action on a manifold induces an action on any function space on that manifold in a straightforward manner. Let [math]X[/math] be a function space on [math]M[/math], such as [math]C^k(M)[/math] or [math]L^p(M)[/math], then the mapping [math]\rho^X:G \times X \to X[/math], defined by

[[math]] \begin{equation} \label{eq:induced_action} \left(\rho^X (g, f)\right)(p) = f(g^{-1}\cdot p) = f(\rho(g^{-1},p)) , \end{equation} [[/math]]

for all [math]f \in X[/math] and [math]g \in G[/math] is a (left) action. We can verify that with

[[math]] \begin{align*} & \rho^X \left( g_2 ,\, \rho^X (g_1,\, f) \right)(p) \\ &= \rho^X(g_1,\,f)(g_2^{-1} \cdot p) \\ &= f \left( g_1^{-1} \cdot (g_2^{-1} \cdot p) \right) \\ &= f \left( (g_1^{-1} g_2^{-1}) \cdot p \right) \\ &= f \left( (g_2 g_1)^{-1} \cdot p \right) \\ &= \rho^X (g_2 g_1,\, f)(p) . \end{align*} [[/math]]

This action on function spaces has the additional property that it is linear in the second argument. We call actions with this property representations of the Lie groups.

Definition (Lie group representation)

Let [math]G[/math] be a Lie group and [math]V[/math] a vector space (finite dimensional or not) then [math]\nu: G \to \rident{Aut}(V)[/math] is a representation of [math]G[/math] if it is a smooth homomorphism, i.e. is smooth and

[[math]] \begin{equation*} \nu(g_1 g_2) = \nu(g_1) \circ \nu(g_2) \qquad \forall g_1,g_2 \in G . \end{equation*} [[/math]]

Recall that the automorphism group Aut([math]V[/math]) is the group of invertible linear transformations of [math]V[/math].

It follows from the definition that a representation [math]\nu[/math] also has the following properties:

[[math]] \begin{equation*} \nu(e) = \mathrm{id}_V \quad\text{and}\quad \nu(g^{-1}) = \nu(g)^{-1}. \end{equation*} [[/math]]

Since we usually only have one group action per manifold, and so one corresponding representation on a given function space we can overload the meaning of the “[math]\cdot[/math]” symbol and use the following equivalent notations:

[[math]] \begin{equation*} g \cdot f := \rho^X_g(f) := \rho^X(g, f) . \end{equation*} [[/math]]

This is how we are going to be modeling transformation acting on our data. In our rotation-translation case [math]f[/math] would be an input image on [math]\mathbb{R}^2[/math] and [math]g \in \iident{SE}(2)[/math] would be a rotation-translation acting on the image.

Equivariant Maps and Operators

Suppose [math]G[/math] is a Lie group and [math]M[/math] and [math]N[/math] are smooth manifolds with smooth (left) actions [math]\rho^M[/math] and [math]\rho^N[/math]. Then we can consider maps [math]F:M \to N[/math] that are equivariant with respect to those group actions, i.e.

[[math]] \begin{equation*} F(\rho^M(g,p)) = \rho^N (g,F(p)) \end{equation*} [[/math]]

for all [math]g \in G[/math] and [math]p \in M[/math], or more concisely:

[[math]] \begin{equation*} F(g \cdot p) = g \cdot F(p). \end{equation*} [[/math]]

Equivalently, [math]F[/math] is equivariant if the following diagram commutes for each [math]g \in G[/math]:

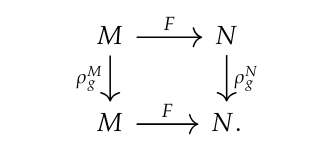
This idea extends naturally to operators between function spaces on those manifolds. Let [math]X[/math] be a function space on [math]M[/math] and [math]Y[/math] a function space on [math]N[/math] equipped with the corresponding representations [math]\rho^X[/math] and [math]\rho^Y[/math] per \ref{eq:induced_action}. Then an operator [math]A:X \to Y[/math] is equivariant if

[[math]] \begin{equation} \label{eq:equivariant_operator} A \circ \rho^X_g = \rho^Y_g \circ A, \qquad \forall g \in G. \end{equation} [[/math]]

Or in words: for every group element doing the corresponding transform on the input space [math]X[/math] and then applying the operator [math]A[/math] gives the same results as first applying the operator [math]A[/math] and then performing the transform corresponding to the group element on the output space [math]Y[/math]. Our goal in the continuous setting is designing our neural network as an equivariant operator that satisfies \ref{eq:equivariant_operator}.

Homogeneous Spaces

While Lie groups represent the transformations we are interested in, homogeneous spaces are the spaces our data will live on and on which the Lie groups will act.

Definition (Homogeneous space)

A smooth manifold [math]M[/math] is a homogeneous space of a Lie group [math]G[/math] if there exists a smooth (left) action [math]\rho:G \times M \to M[/math] that is transitive, i.e.

[[math]] \begin{equation*} \forall p_1,p_2 \in M \ \exists g \in G: \rho(g,p_1)=g \cdot p_1=p_2. \end{equation*} [[/math]]

The elements of [math]M[/math] are called the points of the homogeneous space and [math]G[/math] is called the motion group or the fundamental group of the homogeneous space. The transitive property can be reformulated as: for every point in [math]M[/math] there is a [math]g[/math] that takes us to any other point in [math]M[/math]. Observe that [math]G[/math] is a homogeneous space of itself, called the principal homogeneous space. The group action is just the left multiplication, i.e. [math]\rho_g = L_g[/math]. On the other end we have the trivial homogeneous space consisting of a single element [math]\{ 0 \}[/math], which is a homogeneous space of every Lie group under the identity action [math]\rho(g,0)=0[/math].

[Zero-dimensional manifolds]

You may wonder whether [math]\{0\}[/math] is a manifold. In fact all (at most) countable sets [math]S[/math] are [math]0[/math]-dimensional manifolds. Assign each point [math]p \in S[/math] its own unique chart [math]\varphi_p:\{ p \} \to \mathbb{R}^0=\{ 0 \}[/math]. Since these chart domains do not overlap the charts are trivially smoothly compatible and form a unique smooth atlas.

For each [math]p \in M[/math], the stabilizer or the isotropy group of [math]p[/math] is the subset [math]G_p[/math] of [math]G[/math] (also denoted by [math]\rident{Stab}_G(p)[/math]) that fixes [math]p[/math]:

[[math]] \begin{equation} \label{eq:stabilizer} G_p := \rident{Stab}_G(p) := \left\{ g \in G \ \middle\vert\ g \cdot p = \rho(g,p) = p \right\} . \end{equation} [[/math]]

If we have [math]g_1,g_2 \in G_p[/math] then [math](g_1 g_2) \cdot p = g_1 \cdot (g_2 \cdot p)=g_1 \cdot p=p[/math]. So [math]g_1 g_2 \in G_p[/math], meaning that [math]G_p[/math] is a subgroup of [math]G[/math]. Moreover since the group action is smooth it follows that if [math]\left( g_n \right)_{n\in\mathbb{N}}[/math] is a sequence in [math]G_p[/math] with [math]\lim_{n\to\infty} g_n = g \in G[/math] then

[[math]] \begin{equation*} \rho(g,p) = \rho\left( \lim_{n\to\infty} g_n, p \right) = \lim_{n\to\infty} \rho(g_n,p) = p. \end{equation*} [[/math]]

From which we conclude that [math]g \in G_p[/math] and so [math]G_p[/math] is closed and consequently by Theorem theorem, [math]G_p[/math] is a Lie subgroup of [math]G[/math] for all [math]p \in M[/math].

When we pick a reference element [math]p_0 \in M[/math], we can define the subset [math]G_{p_0,p} \subset G[/math] of all group elements that map [math]p_0[/math] to [math]p[/math]:

[[math]] \begin{equation} G_{p_0,p} := \left\{ g \in G \ \middle\vert \ g \cdot p_0 = p \right\} . \label{eq:homogeneous_set} \end{equation} [[/math]]

Note that this is generally not a subgroup, except for [math]G_{p_0,p_0}=G_{p_0}[/math]. If we have two group elements that map [math]p_0[/math] to the same [math]p[/math], i.e. [math]g_1,g_2 \in G_{p_0,p}[/math] then

[[math]] \begin{equation} \label{eq:homogeneous_equivalence} g_1 \cdot p_0 = g_2 \cdot p_0 \quad \Leftrightarrow\quad g_1^{-1} g_2 \cdot p_0 = p_0 \quad \Leftrightarrow\quad g_1^{-1} g_2 \in G_{p_0}. \end{equation} [[/math]]

This condition imposes an equivalence relation on [math]G[/math], which we can quotient out as follows:

[[math]] \begin{equation*} G/G_{p_0} := \left\{ s \subset G \ \middle\vert\ \forall g_1, g_2 \in s: g_1^{-1} g_2 \in G_{p_0} \right\} = \left\{ G_{p_0,p} \ \middle\vert\ \forall p \in M \right\} . \end{equation*} [[/math]]

There is a straightforward isomorphism between [math]M[/math] and [math]G/G_{p_0}[/math] given by [math]p \mapsto G_{p_0,p}[/math] and [math]G_{p_0,p} \mapsto G_{p_0,p} \cdot p_0[/math]. From which we can conclude that all homogeneous spaces are isomorphic to a Lie group quotient [math]G/H[/math] for some closed Lie subgroup [math]H[/math] of [math]G[/math]. For this reason many authors blur the line between a homogeneous space and its corresponding group quotient and effectively equate a point of the homogeneous space with its corresponding equivalence class in the group, i.e. [math]p \equiv G_{p_0,p}[/math] after fixing a [math]p_0 \in M[/math]. This leads to concise notation such as [math]g \in p \Leftrightarrow g \cdot p_0 = p[/math] and the dropping of the `[math]\cdot[/math]' notation since if [math]p[/math] is seen as a subset of [math]G[/math] then [math]g \cdot p \equiv g p[/math].

General references

Smets, Bart M. N. (2024). "Mathematics of Neural Networks". arXiv:2403.04807 [cs.LG].